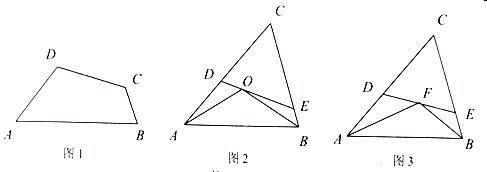
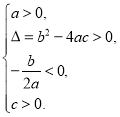题目内容
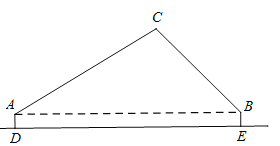
【题目】如图,![]() 的半径为
的半径为![]() ,
,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,连接
上一点,连接![]() 、
、![]() .
.![]() 为劣弧
为劣弧![]() 的中点,过点
的中点,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.

(1)求证:![]() 是
是![]() 的切线;
的切线;
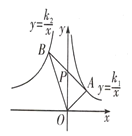
(2)连接![]() ,若
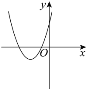
,若![]() ,如图2.
,如图2.
①求![]() 的长;
的长;
②图中阴影部分的面积等于_________.
【答案】(1)见解析;(2)①![]() ,②
,②![]() .
.
【解析】
(1)连接OC,利用等腰三角形三线合一的性质证得OC⊥BF,再根据CG∥FB即可证得结论;
(2)①根据已知条件易证得![]() 是等边三角形,利用三角函数可求得
是等边三角形,利用三角函数可求得![]() 的长,根据三角形重心的性质即可求得答案;
的长,根据三角形重心的性质即可求得答案;
②易证得![]() ,利用扇形的面积公式即可求得答案.
,利用扇形的面积公式即可求得答案.
(1)连接![]() .
.
![]() 是
是![]() 的中点,
的中点,
![]() .
.
又![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() 是
是![]() 的切线.
的切线.

(2)①![]() ,
,
∴![]() .
.
![]() ,
,![]()
![]() .
.
∴![]() 是等边三角形.
是等边三角形.
![]() ,
,![]() ,
,
又![]() 的半径为
的半径为![]() ,
,
在![]() 中,
中,![]() ,
,
∵BF⊥OC,CD⊥OB,BF与CD相交于E,点E是等边三角形OBC的垂心,也是重心和内心,
∴![]() .
.
②∵AF∥BC,
∴![]()
∴ .
.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案【题目】小明将小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度y(m)与它的飞行时间x(s)满足二次函数关系,y与x的几组对应值如下表所示:
x(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
y(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(Ⅰ)求y关于x的函数解析式(不要求写x的取值范围);
(Ⅱ)问:小球的飞行高度能否达到22m?请说明理由.
【题目】关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等且非零的实数根,探究
有两个不相等且非零的实数根,探究![]() 满足的条件.
满足的条件.
小华根据学习函数的经验,认为可以从二次函数的角度研究一元二次方程的根的符号。下面是小华的探究过程:第一步:设一元二次方程![]() 对应的二次函数为
对应的二次函数为![]() ;
;
第二步:借助二次函数图象,可以得到相应的一元二次方程中![]() 满足的条件,列表如下表。
满足的条件,列表如下表。
方程两根的情况 | 对应的二次函数的大致图象 |
|
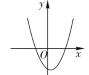
方程有两个不相等的负实根 |
|
|
①_______ |
|
|
方程有两个不相等的正实根 | ② | ③____________ |
(1)请将表格中①②③补充完整;
(2)已知关于![]() 的方程
的方程![]() ,若方程的两根都是正数,求
,若方程的两根都是正数,求![]() 的取值范围.
的取值范围.