题目内容
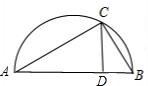 如图所示,AB为半圆的直径,C为半圆上的一点,CD⊥AB于D,若CD=6,AD:DB=3:2,则AC•BC等于________.
如图所示,AB为半圆的直径,C为半圆上的一点,CD⊥AB于D,若CD=6,AD:DB=3:2,则AC•BC等于________.
30
分析:由AB为半圆的直径,得∠ACB=90°,可证△ADC∽△CDB,因此CD2=AD•BD,而CD=6,AD:DB=3:2,可设AD=3x,BD=2x,这样可求出x= ,AD=3
,AD=3  ,BD=
,BD= ,再利用勾股定理求出AC和BC,最后计算它们的积.
,再利用勾股定理求出AC和BC,最后计算它们的积.
解答:∵AB为半圆的直径,
∴∠ACB=90°,
又∵CD⊥AB,
∴△ADC∽△CDB,
∴CD2=AD•BD,而CD=6,AD:DB=3:2,可设AD=3x,BD=2x,
∴36=2x•3x,则x= ,
,
∴AD=3 ,BD=
,BD= ,
,
再利用勾股定理得:
AC= ,BC=
,BC= ,
,
∴AC•BC= ×
× =30
=30  .
.
故答案为:30 .
.
点评:此题主要考查了圆周角定理.同弧所对的圆周角相等,并且等于它所对的圆心角的一半.也考查了直径所对的圆周角为90°和二次根式的计算以及三角形相似的判断.

分析:由AB为半圆的直径,得∠ACB=90°,可证△ADC∽△CDB,因此CD2=AD•BD,而CD=6,AD:DB=3:2,可设AD=3x,BD=2x,这样可求出x=
 ,AD=3
,AD=3  ,BD=
,BD= ,再利用勾股定理求出AC和BC,最后计算它们的积.
,再利用勾股定理求出AC和BC,最后计算它们的积.解答:∵AB为半圆的直径,
∴∠ACB=90°,
又∵CD⊥AB,
∴△ADC∽△CDB,
∴CD2=AD•BD,而CD=6,AD:DB=3:2,可设AD=3x,BD=2x,
∴36=2x•3x,则x=
 ,
,∴AD=3
 ,BD=
,BD= ,
,再利用勾股定理得:
AC=
 ,BC=
,BC= ,
,∴AC•BC=
 ×
× =30
=30  .
.故答案为:30
 .
.点评:此题主要考查了圆周角定理.同弧所对的圆周角相等,并且等于它所对的圆心角的一半.也考查了直径所对的圆周角为90°和二次根式的计算以及三角形相似的判断.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
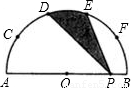
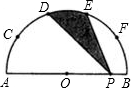 如图所示,AB为半圆O的直径,C、D、E、F是
如图所示,AB为半圆O的直径,C、D、E、F是
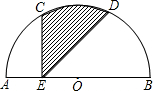 如图所示,AB为半圆的直径,C、D为弧
如图所示,AB为半圆的直径,C、D为弧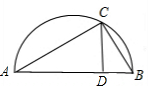 如图所示,AB为半圆的直径,C为半圆上的一点,CD⊥AB于D,若CD=6,AD:DB=3:2,则AC•BC等于
如图所示,AB为半圆的直径,C为半圆上的一点,CD⊥AB于D,若CD=6,AD:DB=3:2,则AC•BC等于 如图所示,AB为半圆的直径,C为半圆上一点,且
如图所示,AB为半圆的直径,C为半圆上一点,且 上的五等分点,P为直径AB上的任意一点,若AB=4,则图中阴影部分的面积为 .
上的五等分点,P为直径AB上的任意一点,若AB=4,则图中阴影部分的面积为 .