题目内容
如图所示，AB为半圆O的直径，C、D、E、F是
上的五等分点，P为直径AB上的任意一点，若AB=4，则图中阴影部分的面积为 ．
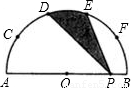
【答案】分析：连接OD、OE，那么阴影部分的面积就等于扇形ODE的面积，根据C、D、E、F是弧AB的五等分点，可求得圆心角∠DOE的度数，进而可根据扇形的面积公式求出阴影部分的面积．
解答：
解：连接OD、OE；
∵C、D、E、F是
上的五等分点，
∴∠DOE=
×180°=36°，
∵△ODE和△PDE同底等高，
∴S扇形DOE=
=
π；
故阴影部分的面积为
π．
点评：此题主要考查的是扇形面积的计算方法，能够发现扇形ODE和阴影部分的面积关系是解决此题的关键．
解答：
解：连接OD、OE；∵C、D、E、F是
上的五等分点，∴∠DOE=
×180°=36°，∵△ODE和△PDE同底等高，
∴S扇形DOE=
=π；故阴影部分的面积为
π．点评：此题主要考查的是扇形面积的计算方法，能够发现扇形ODE和阴影部分的面积关系是解决此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
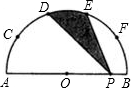如图所示，AB为半圆O的直径，C、D、E、F是
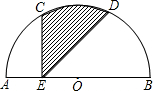如图所示，AB为半圆的直径，C、D为弧
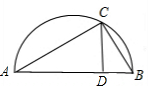如图所示，AB为半圆的直径，C为半圆上的一点，CD⊥AB于D，若CD=6，AD：DB=3：2，则AC•BC等于
如图所示，AB为半圆的直径，C为半圆上一点，且