题目内容
已知:如图,直径为OA的⊙M与x轴交于点O、A,点B、C把弧 CA分为三等份,连接MC并延长交y轴于点D(0,3)

(1)求证:△OMD≌△BAO;
(2)若直线 把⊙M的周长和△OMD面积均分为相等的两部份,求该直线的解析式.
把⊙M的周长和△OMD面积均分为相等的两部份,求该直线的解析式.

(1)求证:△OMD≌△BAO;
(2)若直线
 把⊙M的周长和△OMD面积均分为相等的两部份,求该直线的解析式.
把⊙M的周长和△OMD面积均分为相等的两部份,求该直线的解析式.(1)证明见解析;(2) .
.
 .
.试题分析:(1)连接BM,根据三等份,求出∠1、∠5、∠3、∠2的度数,推出∠1=∠3,根据直径求出∠OBA=∠DOM=90°,根据AAS求出全等即可;
(2)根据面积二等份,推出直线过M和(0,
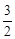 )点,求出OM,得出M的坐标,代入解析式求出即可.
)点,求出OM,得出M的坐标,代入解析式求出即可.试题解析:(1)连接BM,
∵B、C把弧OA三等分,∴∠1=∠5=60°.
∵OM=BM,∴∠2=
 ∠5=30°.
∠5=30°.∵OA为圆M的直径,∴∠ABO="90°." ∴AB=
 OA=OM,∠3="60°." ∴∠1=∠3,∠DOM=∠ABO=90°.
OA=OM,∠3="60°." ∴∠1=∠3,∠DOM=∠ABO=90°.在△OMD和△BAO中,
 ,
,∴△OMD≌△BAO.
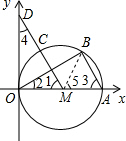
(2)若直线把圆M的面积分为二等份,则直线必过圆心M.
∵D(0,3),∠1=60°,OD=3, tan60°=
 ,∴
,∴ ,即
,即 .
.∴M(
 ,0).
,0).把M(
 ,0)代入y=kx+b,得
,0)代入y=kx+b,得 ,
,又直线平分面积,必过点(0,
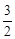 )代入得:
)代入得: ,
,二者联立解得:
 .
.∴直线为
 .
.
练习册系列答案
相关题目

 ,求PO的长.
,求PO的长.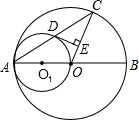

 是
是 的直径,弦
的直径,弦 于点
于点 ,连结
,连结 ,若
,若 ,
, ,则OE=( )
,则OE=( )

