Question

6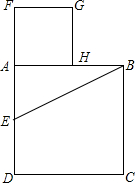．采用如下方法可以得到黄金分割点：如图所示，设AB是已知线段，以AB为边作正方形ABCD；取AD的中点E，连接EB；延长DA至点F，使EF=EB；以线段AF为边作正方形AFGH，点H就是AB的黄金分割点．
任意作一条线段，用上述方法作出这条线段的黄金分割点，你能说说这种作法的道理吗？

Answer 1

分析 设AB=x，根据题意和勾股定理求出BE的长，求出AH：AB，根据黄金比进行解答．

解答 解：设AB=x
∵E是AD的中点，
∴AE=$\frac{1}{2}$x，
由勾股定理得，EB=$\frac{\sqrt{5}}{2}$x，
则AH=AF=$\frac{\sqrt{5}}{2}$x-$\frac{1}{2}$x，
∴AH：AB=$\frac{\sqrt{5}-1}{2}$，
∴点H就是AB的黄金分割点，
∴任意作一条线段，用上述方法作出这条线段的黄金分割点．

点评 本题考查的是黄金分割的概念，掌握黄金比是$\frac{\sqrt{5}-1}{2}$，正确运用勾股定理是解题的关键．