题目内容
3.(1)计算:(π-$\sqrt{3}$)0+($\frac{1}{2}$)-1-$\sqrt{27}$-tan30°;(2)解方程:$\frac{3}{{x}^{2}-9}$+$\frac{x}{x-3}$=1;
(3)解不等式组$\left\{\begin{array}{l}{3y≥y+2}\\{4y-2<y+4}\end{array}\right.$,并把解集在数轴上表示出来.
分析 (1)分别根据0指数幂及负整数指数幂的计算法则、数的开方法则及特殊角的三角函数值计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先把分式方程化为整式方程,求出x的值,在进行检验即可;
(3)分别求出各不等式的解集,再求出其公共解集即可.
解答 解:(1)原式=1+2-3$\sqrt{3}$-$\frac{\sqrt{3}}{3}$
=3-$\frac{10\sqrt{3}}{3}$;
(2)方程两边同时乘以(x+3)(x-3)得,3+x(x+3)=x2-9,
解得x=-4,
代入(x+3)(x-3)得,(-4+3)(-4-3)=7≠0,
故x=-4是原分式方程的解;
(3)$\left\{\begin{array}{l}3y≥y+2①\\ 4y-2<y+4②\end{array}\right.$,
由①得,y≥1,
由②得,y<2,
故不等式组的解集为:1≤y<2.
点评 本题考查的是实数的运算,熟知0指数幂及负整数指数幂的计算法则、数的开方法则及特殊角的三角函数值是解答此题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
13.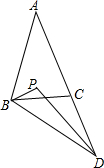 如图,△ABC中,AB=AC,∠A=40°,延长AC到D,使CD=BC,点P是∠ABD和∠ADB的平分线的交点,则∠BPD的度数是( )
如图,△ABC中,AB=AC,∠A=40°,延长AC到D,使CD=BC,点P是∠ABD和∠ADB的平分线的交点,则∠BPD的度数是( )
 如图,△ABC中,AB=AC,∠A=40°,延长AC到D,使CD=BC,点P是∠ABD和∠ADB的平分线的交点,则∠BPD的度数是( )
如图,△ABC中,AB=AC,∠A=40°,延长AC到D,使CD=BC,点P是∠ABD和∠ADB的平分线的交点,则∠BPD的度数是( )| A. | 105° | B. | 110° | C. | 130° | D. | 145° |
14. 如图,直线AB与CD相交于O,E是∠AOD内一点,已知EO⊥AB,垂足为O,且∠BOD=45°,则∠COE的度数是( )
如图,直线AB与CD相交于O,E是∠AOD内一点,已知EO⊥AB,垂足为O,且∠BOD=45°,则∠COE的度数是( )
 如图,直线AB与CD相交于O,E是∠AOD内一点,已知EO⊥AB,垂足为O,且∠BOD=45°,则∠COE的度数是( )
如图,直线AB与CD相交于O,E是∠AOD内一点,已知EO⊥AB,垂足为O,且∠BOD=45°,则∠COE的度数是( )| A. | 115° | B. | 125° | C. | 135° | D. | 145° |
11.下列调查适合抽样调查的是( )
| A. | 审核书稿中的错别字 | B. | 对某社区的卫生死角进行调查 | ||
| C. | 对八名同学的身高情况进行调查 | D. | 对中学生目前的睡眠情况进行调查 |
18.已知边长为m的正方形面积为12,则下列关于m的说法中,错误的是( )
①m是无理数;
②m是方程m2-12=0的解;
③m满足不等式组$\left\{\begin{array}{l}{m-4>0}\\{m-5<0}\end{array}\right.$;
④m是12的算术平方根.
①m是无理数;
②m是方程m2-12=0的解;
③m满足不等式组$\left\{\begin{array}{l}{m-4>0}\\{m-5<0}\end{array}\right.$;
④m是12的算术平方根.
| A. | ①② | B. | ①③ | C. | ③ | D. | ①②④ |
8.下列事件中,属于必然事件的是( )
| A. | 明天我市下雨 | |
| B. | 抛一枚硬币,正面朝下 | |
| C. | 购买一张福利彩票中奖了 | |
| D. | 掷一枚骰子,向上一面的数字一定大于零 |
15. 如图,探索下列规律,根据规律,从2014到2016箭头的方向是( )
如图,探索下列规律,根据规律,从2014到2016箭头的方向是( )
 如图,探索下列规律,根据规律,从2014到2016箭头的方向是( )
如图,探索下列规律,根据规律,从2014到2016箭头的方向是( )| A. | ↓→ | B. | →↑ | C. | ↑→ | D. | →↓ |
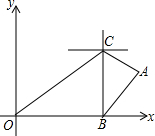 中国派遣三艘海监船在南海保护中国渔民不受菲律宾的侵犯.在雷达显示图上,标明了三艘海监船的坐标为O(0,0)、B(80,0)、C(80,60),(单位:海里)三艘海监船安装有相同的探测雷达,雷达的有效探测范围是半径为r的圆形区域(只考虑在海平面上的探测).
中国派遣三艘海监船在南海保护中国渔民不受菲律宾的侵犯.在雷达显示图上,标明了三艘海监船的坐标为O(0,0)、B(80,0)、C(80,60),(单位:海里)三艘海监船安装有相同的探测雷达,雷达的有效探测范围是半径为r的圆形区域(只考虑在海平面上的探测).