Question

（1）如图，在△AFD和△BEC中，点A、E、F、C在同一直线上，AD=CB，AE=CF，∠A=∠C．求证：△AFD≌△BEC．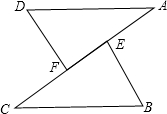

（2）如图：△ABC中，AB=AC=4，∠BAC=120°，D为BC中点，DE⊥AC，求AE的长．

Answer 1

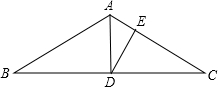
分析：（1）本题需先证出AF=CE，再根据SAS，即可得出△ADF≌△CBE．
（2）本题需先求出∠B=∠C=30°，再证出∠DAC=60°，从而得出∠ADE=30°，最后求出AE的长．

解答：解：（1）证明：∵AE=CF
又∵AF=AE+EFCE=CF+EF
∴AF=CE，
在△ADF与△CBE中

AD=CB ∠A=∠C AF=CE

，
∴△ADF≌△CBE（SAS），

（2）证明：∵AB=AC=4，∠BAC=120°
∴∠B=∠C=

180°-120°

2

=30°
∵D为BC中点AB=AC
∴AD⊥BC
∴AD=

1

2

AB=2，
∴∠BAD=90°-30°=60°∠BAC=120°
∴∠DAC=60°
又∵DE⊥AC
∴∠ADE=30°，
∴AE=

1

2

AD=1．

点评：本题主要考查了全等三角形的判定，在解题时要能灵活应用全等三角形的判定和等腰三角形的性质是本题的关键．