Question

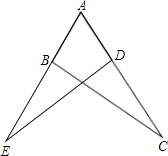
【题目】如图，正方形ABCD中，E，F分别为BC，CD上的点，且AE⊥BF，垂足为G．

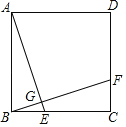
（1）求证：AE＝BF；（2）若BE＝，AG＝2，求正方形的边长．

Answer 1

【答案】（1）见解析；（2）正方形的边长为.

【解析】

（1）由正方形的性质得出AB＝BC，∠ABC＝∠C＝90°，∠BAE+∠AEB＝90°，由AE⊥BF，得出∠CBF+∠AEB＝90°，推出∠BAE＝∠CBF，由ASA证得△ABE≌△BCF即可得出结论；

（2）证出∠BGE＝∠ABE＝90°，∠BEG＝∠AEB，得出△BGE∽△ABE，得出BE2＝EGAE，设EG＝x，则AE＝AG+EG＝2+x，代入求出x，求得AE＝3，由勾股定理即可得出结果．

（1）证明：∵四边形ABCD是正方形，

∴AB＝BC，∠ABC＝∠C＝90°，

∴∠BAE+∠AEB＝90°，

∵AE⊥BF，垂足为G，

∴∠CBF+∠AEB＝90°，

∴∠BAE＝∠CBF，

在△ABE与△BCF中，

，

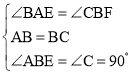∴△ABE≌△BCF（ASA），

∴AE＝BF；

（2）解：∵四边形ABCD为正方形，

∴∠ABC＝90°，

∵AE⊥BF，

∴∠BGE＝∠ABE＝90°，

∵∠BEG＝∠AEB，

∴△BGE∽△ABE，

∴＝，

即：BE2＝EGAE，

设EG＝x，则AE＝AG+EG＝2+x，

∴（）2＝x（2+x），

解得：x1＝1，x2＝﹣3（不合题意舍去），

∴AE＝3，

∴AB＝＝＝．