题目内容
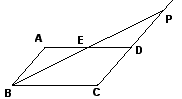
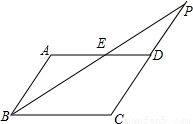
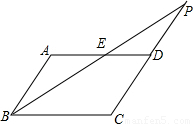
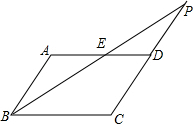
己知:如图,点P为平行四边形ABCD中CD边的延长线上一点,连接BP,交AD,于点E,探究:当PD与CD有什么数量关系时,△ABE≌△DPE.画出图形并证明△ABE≌△DPE.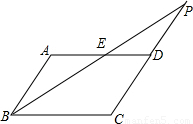
【答案】分析:当PD=CD时,△ABE≌△DPE.由平行四边形性质得出各边关系,继而可证△ABE≌△DPE.
解答: 解:当PD=CD时,△ABE≌△DPE.
解:当PD=CD时,△ABE≌△DPE.
画出图形如图:
证明:∵四边形ABCD是平行四边形
∴AB=CD,AB∥CD,
∴∠BAE=∠PDE,
又∵PD=CD,
∴AB=DP,
在△ABE和△DPE中
∴△ABE≌△DPE中(AAS).
点评:本题主要考查了平行四边形性质和全等三角形的判定,难度中等
解答:
 解:当PD=CD时,△ABE≌△DPE.
解:当PD=CD时,△ABE≌△DPE.画出图形如图:
证明:∵四边形ABCD是平行四边形
∴AB=CD,AB∥CD,
∴∠BAE=∠PDE,
又∵PD=CD,
∴AB=DP,
在△ABE和△DPE中

∴△ABE≌△DPE中(AAS).
点评:本题主要考查了平行四边形性质和全等三角形的判定,难度中等

练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
 己知:如图,点P为平行四边形ABCD中CD边的延长线上一点,连接BP,交AD,于点E,探究:当PD与CD有什么数量关系时,△ABE≌△DPE.画出图形并证明△ABE≌△DPE.
己知:如图,点P为平行四边形ABCD中CD边的延长线上一点,连接BP,交AD,于点E,探究:当PD与CD有什么数量关系时,△ABE≌△DPE.画出图形并证明△ABE≌△DPE. 己知:如图,点P为平行四边形ABCD中CD边的延长线上一点,连接BP,交AD,于点E,探究:当PD与CD有什么数量关系时,△ABE≌△DPE.画出图形并证明△ABE≌△DPE.
己知:如图,点P为平行四边形ABCD中CD边的延长线上一点,连接BP,交AD,于点E,探究:当PD与CD有什么数量关系时,△ABE≌△DPE.画出图形并证明△ABE≌△DPE.