题目内容
2.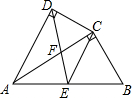 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB中点,
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB中点,(1)求证:AC2=AB•AD;
(2)猜想:AD与CE的位置关系是AD∥CE,并证明;
(3)若AD=4,AB=6,求$\frac{AC}{AF}$的值.
分析 (1)由AC平分∠DAB,∠ADC=∠ACB=90°,可证得△ADC∽△ACB,然后由相似三角形的对应边成比例,证得AC2=AB•AD;
(2)由E为AB的中点,根据在直角三角形中,斜边上的中线等于斜边的一半,即可证得CE=$\frac{1}{2}$AB=AE,继而可证得∠DAC=∠ECA,得到CE∥AD;
(3)易证得△AFD∽△CFE,然后由相似三角形的对应边成比例,求得$\frac{AC}{AF}$的值.
解答 解:(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB.
又∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB.
∴AD:AC=AC:AB,
∴AC2=AB•AD.
(2)证明:∵E为AB的中点,∠ACB=90°,
∴CE=$\frac{1}{2}$AB=AE.
∴∠EAC=∠ECA.
∵∠DAC=∠CAB,
∴∠DAC=∠ECA.
∴AD∥CE.
故答案为:AD∥CE.
(3)解:∵CE∥AD,
∴△AFD∽△CFE,
∴AD:CE=AF:CF,
∵CE=$\frac{1}{2}$AB,
∴CE=$\frac{1}{2}$×6=3,
∵AD=4,
∴$\frac{4}{3}$=$\frac{AF}{CF}$,
∴$\frac{AC}{AF}$=$\frac{7}{4}$.
点评 此题考查了相似三角形的判定与性质、等腰三角形的性质以及直角三角形的性质,利用直角三角形斜边上中线的性质得到CE=$\frac{1}{2}$AB是解题的关键.

练习册系列答案
相关题目
12. 如图,a∥b,∠1=55°,∠2=120°,则∠3的度数是( )
如图,a∥b,∠1=55°,∠2=120°,则∠3的度数是( )
 如图,a∥b,∠1=55°,∠2=120°,则∠3的度数是( )
如图,a∥b,∠1=55°,∠2=120°,则∠3的度数是( )| A. | 55° | B. | 60° | C. | 65° | D. | 70° |
10.在?ABCD中,∠ABC的平分线BE于边AD交于点E,与对角线AC交于点O,点E将边AD分成3:2两部分,则△AOE与△BOC的面积之比为( )
| A. | 4:9或9:25 | B. | 9:25或4:25 | C. | 2:5 | D. | 3:5 |
12.下列各式中,y是x的二次函数的是( )
| A. | y=2x+1 | B. | y=-2x+1 | C. | y=x2+2 | D. | y=$\frac{1}{2}$x-2 |



