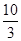题目内容
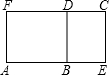
如图所示，已知矩形AECF∽矩形BECD，且AF=FD，那么AE与AF的比值是（ ）
A．
| B．
| C．
| D．
|
设AF=FD=y，DC=x，根据题意得
=
，
整理得
-
-1=0，
设
=t，
原方程可化为：t-
-1=0，
即t2-t-1=0，
解得t=
（负值舍去）或t=
．
由于两四边形相似，所以AE与AF的比值是
=t=（1+
）：2．
故选C．
| x+y |
| y |
| y |
| x |
整理得
| y |
| x |
| x |
| y |
设
| y |
| x |
原方程可化为：t-
| 1 |
| t |
即t2-t-1=0，
解得t=
1-
| ||
| 2 |
1+
| ||
| 2 |
由于两四边形相似，所以AE与AF的比值是
| y |
| x |
| 5 |
故选C．
练习册系列答案
相关题目
的中点，连接BD并延长BD到点E，使BD=DE，连接CD和DE．
