题目内容
 如图在边长为2的正方形ABCD中,E,F,O分别是AB,CD,AD的中点,以O为圆心,以OE为半径画弧EF.P是
如图在边长为2的正方形ABCD中,E,F,O分别是AB,CD,AD的中点,以O为圆心,以OE为半径画弧EF.P是 |
| EF |
| BG |
| BM |
分析:根据MG与⊙O相切得OK⊥MG.设直线OK交AB的延长线于点H,易证∠MGB=∠BHK.根据三角函数定义,tan∠MGB=tan∠BHK=
=
,从而有AH=3,BH=3BK.因为AB=2,所以BH=1,可求BK.
P为动点,当P接近F点时,本题另有一个解.
| BM |
| BG |
| 1 |
| 3 |
P为动点,当P接近F点时,本题另有一个解.
解答:解:(1)若OP的延长线与射线AB的延长线相交,设交点为H.如图1,
∵MG与⊙O相切,
∴OK⊥MG.
∵∠BKH=∠PKG,
∴∠MGB=∠BHK.
∵
=3,
∴tan∠BHK=
.
∴AH=3AO=3×1=3,
BH=3BK.
∵AB=2,
∴BH=1,
∴BK=
.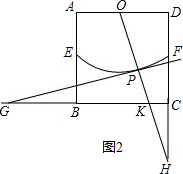
(2)若OP的延长线与射线DC的延长线相交,设交点为H.如图2,
同理可求得BK=
.
综上所述,本题应填
,
.

∵MG与⊙O相切,
∴OK⊥MG.
∵∠BKH=∠PKG,
∴∠MGB=∠BHK.
∵
| BG |
| BM |
∴tan∠BHK=
| 1 |
| 3 |
∴AH=3AO=3×1=3,
BH=3BK.
∵AB=2,
∴BH=1,
∴BK=
| 1 |
| 3 |

(2)若OP的延长线与射线DC的延长线相交,设交点为H.如图2,
同理可求得BK=
| 5 |
| 3 |
综上所述,本题应填
| 1 |
| 3 |
| 5 |
| 3 |
点评:此题考查了切线的性质及三角函数等知识点,综合性强,难度较大.
本题需要特别注意有2个解,不要漏解.
本题需要特别注意有2个解,不要漏解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P. 如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.