Question

【题目】在平面直角坐标系中，点A1，A2，A3和B1，B2，B3分别在直线y=和x轴上，△OA1B1，△B1A2B2，△B2A3B3都是等腰直角三角形．则A3的坐标为_______.

．

Answer 1

【答案】A3（）

【解析】

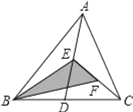
设直线y=与x轴的交点为G，过点A1，A2，A3分别作x轴的垂线，垂足分别为D、E、F，由条件可求得，再根据等腰三角形可分别求得A1D、A2E、A3F，可得到A1，A2，A3的坐标.

设直线y=与x轴的交点为G，
令y=0可解得x=-4，
∴G点坐标为（-4，0），
∴OG=4，
如图1，过点A1，A2，A3分别作x轴的垂线，垂足分别为D、E、F，

∵△A1B1O为等腰直角三角形，
∴A1D=OD，
又∵点A1在直线y=x+上，
∴=，即=，

解得A1D=1=（）0，
∴A1（1，1），OB1=2，
同理可得=，即=，

解得A2E=

=（）1，则OE=OB1+B1E=，
∴A2（，），OB2=5，
同理可求得A3F=

=（）2，则OF=5+=，
∴A3（，）；

故答案为：（，）