Question

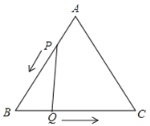
【题目】已知：如图，△ABC中，AB=AC=6，∠A=45°，点D在AC上，点E在BD上，且△ABD、△CDE、△BCE均为等腰三角形．

（1）求∠EBC的度数；

（2）求BE的长．

Answer 1

【答案】（1）22.5°；（2）6﹣6．

【解析】

试题（1）由AB=AC=6，∠A=45°，可求得∠ABC的度数，又由AD=BD，可求得∠ABD的度数，继而求得答案；

（2）由AB=AC=6，∠A=45°，可求得BD的长，然后设DE=EC=x，可得BE=EC=x，即可得方程x+x=3，继而求得答案．

解：（1）∵AB=AC=6，∠A=45°，

∴∠ABC=∠ACB=67.5°，

∵△ABD是等腰三角形，AD=BD，

∴∠ABD=∠A=45°，

∴∠EBC=∠ABC﹣∠ABD=22.5°；

（2）∵∠A=∠ABD=45°，

∴∠ADB=∠CDE=90°，

∵AB=6，

∴BD=ABcos45°=3，

设DE=x，则CD=DE=x，

∴EC==x，

∵BE=EC=x，

∴x+x=3，

解得：x=6﹣3，

∴BE=6﹣6．