题目内容
如图(1),AD,AE分别是△ABC中BC边上的高和中线,已知AD=5cm,EC=2cm.
(1)求△ABE和△AEC的面积;
(2)通过做题,你能发现什么结论?请说明理由.
(3)根据(2)中的结论,解决下列问题:如图(2),CD是△ABC的中线,DE是△ACD的中线,EF是△ADE的中线,若△AEF的面积为1cm2,求△ABC的面积.

(1)求△ABE和△AEC的面积;
(2)通过做题,你能发现什么结论?请说明理由.
(3)根据(2)中的结论,解决下列问题:如图(2),CD是△ABC的中线,DE是△ACD的中线,EF是△ADE的中线,若△AEF的面积为1cm2,求△ABC的面积.

分析:(1)根据三角形中线的定义得到BE=EC=2cm,然后根据三角形的面积公式计算△ABE和△AEC的面积;
(2)根据计算的结果得到等底等高的三角形的面积相等;
(3)根据等底等高的三角形的面积相等先得到S△ADE=2cm2,再得到S△DEC=S△ADE=2cm2,则S△ADC=4cm2,然后根据结论得到S△BDC=S△ADC=4cm2,所以S△ABC=8cm2.
(2)根据计算的结果得到等底等高的三角形的面积相等;
(3)根据等底等高的三角形的面积相等先得到S△ADE=2cm2,再得到S△DEC=S△ADE=2cm2,则S△ADC=4cm2,然后根据结论得到S△BDC=S△ADC=4cm2,所以S△ABC=8cm2.
解答:解:(1)∵AE是△ABC中BC边上的中线,
∴BE=EC=2cm,
∴S△ABE=
×BE×AD=
×2×5=5(cm2);S△AEC=
×EC×AD=
×2×5=5(cm2);
(2)等底等高的三角形的面积相等;
(3)∵EF是△ADE的中线,若△AEF的面积为1cm2,
∴S△DFE=S△AEF=1cm2,
∴S△ADE=2cm2,
∵DE是△ACD的中线,
∴S△DEC=S△ADE=2cm2,
∴S△ADC=4cm2,
∵CD是△ABC的中线,
∴S△BDC=S△ADC=4cm2,
∴S△ABC=8cm2.
∴BE=EC=2cm,
∴S△ABE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)等底等高的三角形的面积相等;
(3)∵EF是△ADE的中线,若△AEF的面积为1cm2,
∴S△DFE=S△AEF=1cm2,
∴S△ADE=2cm2,
∵DE是△ACD的中线,
∴S△DEC=S△ADE=2cm2,
∴S△ADC=4cm2,
∵CD是△ABC的中线,
∴S△BDC=S△ADC=4cm2,
∴S△ABC=8cm2.
点评:本题考查了三角形的面积:三角形的面积等于底边长与高线乘积的一半,即S△=
×底×高.三角形的中线将三角形分成面积相等的两部分.
| 1 |
| 2 |

练习册系列答案
相关题目
 9、已知:如图在△ABC中,AD平分∠BAC,AD⊥BC,则△ACD≌△ABD的根据是
9、已知:如图在△ABC中,AD平分∠BAC,AD⊥BC,则△ACD≌△ABD的根据是 18、如图,∠C=90°,AD平分∠BAC,DE⊥AB于E,则BC=DB+CD=DB+
18、如图,∠C=90°,AD平分∠BAC,DE⊥AB于E,则BC=DB+CD=DB+ 24、如图,△ABC中,AD为BC边上的高,点E在AC边上,BE交AD于点F,若BF=AC,FD=CD,
24、如图,△ABC中,AD为BC边上的高,点E在AC边上,BE交AD于点F,若BF=AC,FD=CD,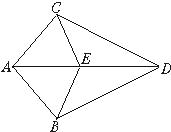 4、如图,AC=AB,AD平分∠CAB,E在AD上,则图中能全等的三角形有( )对.
4、如图,AC=AB,AD平分∠CAB,E在AD上,则图中能全等的三角形有( )对. 如图,AB∥CD,AD与BC相交于点O,
如图,AB∥CD,AD与BC相交于点O,