题目内容
菱形ABCD中,如果 AB2=BD•AC,则∠ABC的度数是
AB2=BD•AC,则∠ABC的度数是
- A.60°
- B.30°
- C.60°或120°
- D.30°或150°
C
分析:首先设AB=a,由四边形ABCD是菱形,即可求得OA2+OB2=AB2=a2,又由 AB2=BD•AC,易求得OA•OB=
AB2=BD•AC,易求得OA•OB= a2,继而求得OA+OB=
a2,继而求得OA+OB= a,则可知OA,OB是方程:x2-
a,则可知OA,OB是方程:x2- ax+
ax+ a=0的解,继而求得OA的值,然后利用特殊角的三角函数值,求得∠ABC的度数.
a=0的解,继而求得OA的值,然后利用特殊角的三角函数值,求得∠ABC的度数.
解答: 解:设AB=a,
解:设AB=a,
∵四边形ABCD是菱形,
∴AC⊥BD,OA= AC,OB=
AC,OB= BD,
BD,
∴在Rt△AOB中,OA2+OB2=AB2=a2,
∵ AB2=BD•AC=4OA•OB=
AB2=BD•AC=4OA•OB= a2,
a2,
∴OA•OB= a2,
a2,
∴(OA+OB)2=OA2+OB2+2OA•OB=a2+ a2=
a2=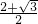 a2,
a2,
∴OA+OB= a,
a,
∴OA,OB是方程:x2- ax+
ax+ a=0的解,
a=0的解,
解得:x1= ,x2=
,x2= a,
a,
当OA= a时,sin∠ABO=
a时,sin∠ABO=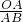 =
= ,
,
∴∠ABO=30°,
∴∠ABC=2∠ABO=60°;
当OA= a时,sin∠ABO=
a时,sin∠ABO=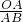 =
= ,
,
∴∠ABO=60°,
∴∠ABC=2∠ABO=120°.
∴∠ABC的度数是:60°或120°.
故选C.
点评:此题考查了菱形的性质、勾股定理、特殊角的三角函数值以及一元二次方程的根与系数的关系.此题难度较大,注意掌握数形结合思想、方程思想与分类讨论思想的应用.
分析:首先设AB=a,由四边形ABCD是菱形,即可求得OA2+OB2=AB2=a2,又由
 AB2=BD•AC,易求得OA•OB=
AB2=BD•AC,易求得OA•OB= a2,继而求得OA+OB=
a2,继而求得OA+OB= a,则可知OA,OB是方程:x2-
a,则可知OA,OB是方程:x2- ax+
ax+ a=0的解,继而求得OA的值,然后利用特殊角的三角函数值,求得∠ABC的度数.
a=0的解,继而求得OA的值,然后利用特殊角的三角函数值,求得∠ABC的度数.解答:
 解:设AB=a,
解:设AB=a,∵四边形ABCD是菱形,
∴AC⊥BD,OA=
 AC,OB=
AC,OB= BD,
BD,∴在Rt△AOB中,OA2+OB2=AB2=a2,
∵
 AB2=BD•AC=4OA•OB=
AB2=BD•AC=4OA•OB= a2,
a2,∴OA•OB=
 a2,
a2,∴(OA+OB)2=OA2+OB2+2OA•OB=a2+
 a2=
a2=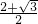 a2,
a2,∴OA+OB=
 a,
a,∴OA,OB是方程:x2-
 ax+
ax+ a=0的解,
a=0的解,解得:x1=
 ,x2=
,x2= a,
a,当OA=
 a时,sin∠ABO=
a时,sin∠ABO=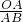 =
= ,
,∴∠ABO=30°,
∴∠ABC=2∠ABO=60°;
当OA=
 a时,sin∠ABO=
a时,sin∠ABO=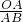 =
= ,
,∴∠ABO=60°,
∴∠ABC=2∠ABO=120°.
∴∠ABC的度数是:60°或120°.
故选C.
点评:此题考查了菱形的性质、勾股定理、特殊角的三角函数值以及一元二次方程的根与系数的关系.此题难度较大,注意掌握数形结合思想、方程思想与分类讨论思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目