题目内容
 如图,在某海域内有三个港口A、D、C.港口C在港口A北偏东60°方向上,港口D在港口A北偏西60°方向上.一艘船以每小时25海里的速度沿北偏东30°的方向驶离A港口3小时后到达B点位置处,此时发现船舱漏水,海水以每5分钟4吨的速度渗入船内.当船舱渗入的海水总量超过75吨时,船将沉入海中.同时在B处测得港口C在B处的南偏东75°方向上.若船上的抽水机每小时可将8吨的海水排出船外,问此船在B处至少应以怎样的航行速度驶向最近的港口停靠,才能保证船在抵达港口前不会沉没(要求计算结果保留根号)?并指出此时船的航行方向.
如图,在某海域内有三个港口A、D、C.港口C在港口A北偏东60°方向上,港口D在港口A北偏西60°方向上.一艘船以每小时25海里的速度沿北偏东30°的方向驶离A港口3小时后到达B点位置处,此时发现船舱漏水,海水以每5分钟4吨的速度渗入船内.当船舱渗入的海水总量超过75吨时,船将沉入海中.同时在B处测得港口C在B处的南偏东75°方向上.若船上的抽水机每小时可将8吨的海水排出船外,问此船在B处至少应以怎样的航行速度驶向最近的港口停靠,才能保证船在抵达港口前不会沉没(要求计算结果保留根号)?并指出此时船的航行方向.
分析:本题是将实际问题转化为直角三角形中的数学问题,可通过构造出与实际问题有关的直角三角形,利用题中已知角和边,借助于三角函数来求解.
解答: 解:连接AC、AD、BC、BD,延长AT,
解:连接AC、AD、BC、BD,延长AT,
过B作BT⊥AT于T,AC与BT交于点E.
过B作BP⊥AC于点P.
由已知得∠BAD=90°,∠BAC=30°,AB=3×25=75(海里),
在△BEP和△AET中,∠BPE=∠ATE=90°,∠AET=∠BEP,
∴∠EBP=∠EAT=30度.
∵∠BAT=60°,∴∠BAP=30°,从而BP=
×75=37.5(海里).
∵港口C在B处的南偏东75°方向上,∴∠CBP=45度.
在等腰Rt△CBP中,BC=
BP=
(海里),
∴BC<AB.
∵△BAD是Rt△,∴BD>AB.
综上,可得港口C离B点位置最近.∴此船应转向南偏东75°方向上直接驶向港口C.
设由B驶向港口C船的速度为每小时x海里,
则据题意应有
(60÷5×4-8)<75,
解不等式,得:x>20
(海里).
答:此船应转向沿南偏东75°的方向向港口C航行,且航行速度至少不低于每小时20
海里,才能保证船在抵达港口前不会沉没.
 解:连接AC、AD、BC、BD,延长AT,
解:连接AC、AD、BC、BD,延长AT,过B作BT⊥AT于T,AC与BT交于点E.
过B作BP⊥AC于点P.
由已知得∠BAD=90°,∠BAC=30°,AB=3×25=75(海里),
在△BEP和△AET中,∠BPE=∠ATE=90°,∠AET=∠BEP,
∴∠EBP=∠EAT=30度.
∵∠BAT=60°,∴∠BAP=30°,从而BP=
| 1 |
| 2 |
∵港口C在B处的南偏东75°方向上,∴∠CBP=45度.
在等腰Rt△CBP中,BC=
| 2 |
75
| ||
| 2 |
∴BC<AB.
∵△BAD是Rt△,∴BD>AB.
综上,可得港口C离B点位置最近.∴此船应转向南偏东75°方向上直接驶向港口C.
设由B驶向港口C船的速度为每小时x海里,
则据题意应有
| ||||
| x |
解不等式,得:x>20
| 2 |
答:此船应转向沿南偏东75°的方向向港口C航行,且航行速度至少不低于每小时20
| 2 |
点评:根据题意准确画出示意图是解这类题的前提和保障.可通过作辅助线构造直角三角形,再把条件和问题转化到直角三角形中,使问题得以解决.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 B处至少应以怎样的航行速度驶向最近的港口停靠,才能保证船在抵达港口前不会沉没(要求计算结果保留根号)?
B处至少应以怎样的航行速度驶向最近的港口停靠,才能保证船在抵达港口前不会沉没(要求计算结果保留根号)?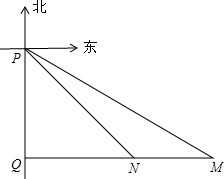 ,P、M两港口相距20海里,P、N两港口相距10
,P、M两港口相距20海里,P、N两港口相距10 (2012•本溪二模)如图,在某海域内有三个港口A、C、D.港口C在港口A北偏东60°方向上,港口D在港口A北偏西60°方向上.一艘船以每小时25海里的速度沿北偏东30°的方向驶离A港口3小时后到达B点位置处,此时发现船舱漏水,同时在B处测得港口C在B处的南偏东75°方向上.若此船在B处向最近的港口停靠,应向A、C、D三个港口中的哪个港口停靠?并说明理由.
(2012•本溪二模)如图,在某海域内有三个港口A、C、D.港口C在港口A北偏东60°方向上,港口D在港口A北偏西60°方向上.一艘船以每小时25海里的速度沿北偏东30°的方向驶离A港口3小时后到达B点位置处,此时发现船舱漏水,同时在B处测得港口C在B处的南偏东75°方向上.若此船在B处向最近的港口停靠,应向A、C、D三个港口中的哪个港口停靠?并说明理由. 海里.求:
海里.求: