Question

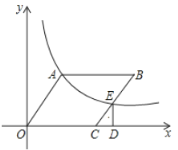
【题目】如图，在平面直角坐标系中，的顶点的坐标为反比例函数的图象经过点且交于点过点作轴于点．

（1）求反比例函数的解析式；

（2）若点是反比例函数图象上一点，且的面积等于面积的，求点的坐标．

Answer 1

【答案】（1）；（2）或

【解析】

（1）利用平行线的性质得到∠ECD＝45，则CD＝DE＝1，则可确定E点坐标，然后根据反比例函数图象上点的坐标特征可求出k的值；

（2）作AH⊥x轴于H，如图，易得A（2，2），则可求出S平行四边形ABCO＝6，设F（t，），利用平行四边形的性质得AB∥OC，AB＝OC＝3，然后根据三角形面积公式得到3|﹣2|＝6，再解绝对值方程求出t即可得到F点的坐标．

四边形为平行四边形，

在中，

把代入中，得

反比例函数的解析式为；

如解图，过点作轴于点

设则

解得(负值舍去)，

设

四边形为平行四边形，

的面积等于面积的

解得

点的坐标为或