题目内容
【题目】在平面直角坐标系![]() 中,对于图形
中,对于图形![]() ,若存在一个正方形
,若存在一个正方形![]() ,这个正方形的某条边与
,这个正方形的某条边与![]() 轴垂直,且图形
轴垂直,且图形![]() 上的所有的点都在该正方形的内部或者边上,则称该正方形
上的所有的点都在该正方形的内部或者边上,则称该正方形![]() 为图形
为图形![]() 的一个正覆盖.很显然,如果图形
的一个正覆盖.很显然,如果图形![]() 存在一个正覆盖,则它的正覆盖有无数个,我们将图形
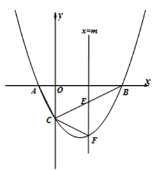
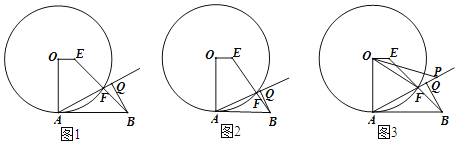
存在一个正覆盖,则它的正覆盖有无数个,我们将图形![]() 的所有正覆盖中边长最小的一个,称为它的紧覆盖,如图所示,图形
的所有正覆盖中边长最小的一个,称为它的紧覆盖,如图所示,图形![]() 为三条线段和一个圆弧组成的封闭图形,图中的三个正方形均为图形
为三条线段和一个圆弧组成的封闭图形,图中的三个正方形均为图形![]() 的正覆盖,其中正方形
的正覆盖,其中正方形![]() 就是图形
就是图形![]() 的紧覆盖.
的紧覆盖.
(1)对于半径为2的![]() ,它的紧覆盖的边长为____.
,它的紧覆盖的边长为____.
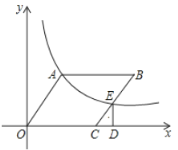
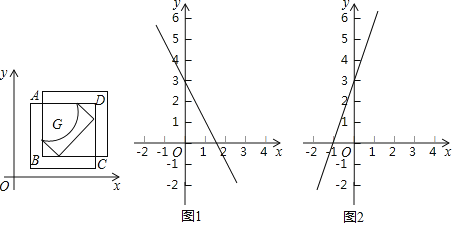
(2)如图1,点![]() 为直线
为直线![]() 上一动点,若线段
上一动点,若线段![]() 的紧覆盖的边长为
的紧覆盖的边长为![]() ,求点
,求点![]() 的坐标.
的坐标.
(3)如图2,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]()
①以![]() 为圆心,
为圆心,![]() 为半径的
为半径的![]() 与线段
与线段![]() 有公共点,且由
有公共点,且由![]() 与线段
与线段![]() 组成的图形
组成的图形![]() 的紧覆益的边长小于
的紧覆益的边长小于![]() ,直接写出
,直接写出![]() 的取值范围;
的取值范围;
②若在抛物线![]() 上存在点
上存在点![]() ,使得
,使得![]() 的紧覆益的边长为
的紧覆益的边长为![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)4;(2)(![]() ,2)或(2,-1);(3)①
,2)或(2,-1);(3)①![]() ≤r<1;②a≥
≤r<1;②a≥![]() 或a≤-2.
或a≤-2.
【解析】
(1)由题意半径为2的⊙O的外切正方形是半径为2的⊙O紧覆盖,由此即可解决问题;
(2)由题意当点P到坐标轴的距离等于2时,线段OP的紧覆盖的正方形的边长为2.分两种情形分别求解即可;
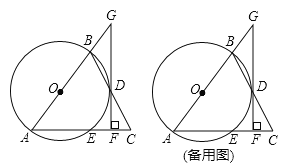
(3)①如图2中,作OH⊥AB于H.利用两种特殊位置解决问题即可;
②如图2-1中,由题意当抛物线与图中矩形EFGH区域有交点时,在抛物线y=ax2+2ax-2(a≠0)上存在点C,使得△ABC的紧覆益的边长为3;
(1)由题意半径为2的⊙O的外切正方形是半径为2的⊙O紧覆盖,
∴紧覆盖的边长为4,
故答案为4.
(2)由题意当点P到坐标轴的距离等于2时,线段OP的紧覆盖的边长为2.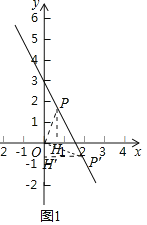
①当点P在第一象限时,作PH⊥x轴于H则PH=2,
y=2时,2=-2x+3,
x=![]() ,
,
∴P(![]() ,2).
,2).
②当点P′在第三象限时,作P′H′⊥y轴,则P′H′=2,
当x=2时,y=-1,
∴P′(2,-1).
综上所述,满足条件的点P坐标为(![]() ,2)或(2,-1).
,2)或(2,-1).
(3)①如图2中,作OH⊥AB于H.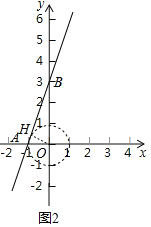
由题意A(-1,0),B(0,3),
∴OA=1,OB=3,AB=![]() ,
,
∵![]() OAOB=
OAOB=![]() ABOH,
ABOH,
∴OH=![]() ,
,
当⊙O经过点A时,r=1,此时由⊙O与线段AB组成的图形G的紧覆益的边长为4,
观察图象可知满足条件的r的范围为:![]() ≤r<1.
≤r<1.
②如图2-1中,如图由题意当抛物线与图中矩形EFGH区域有交点时,在抛物线y=ax2+2ax-2(a≠0)上存在点C,使得△ABC的紧覆益的边长为3.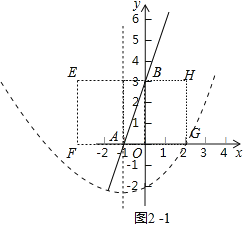
由题意E(-3,3),F(-3,0),G(2
当抛物线经过点G时,4a+4a-2=0,
∴a=![]() ,
,
∵抛物线的对称轴x=-1,经过(0,-2),
观察图象可知,当a≥![]() 时,在抛物线y=ax2+2ax-2(a≠0)上存在点C,使得△ABC的紧覆益的边长为3.
时,在抛物线y=ax2+2ax-2(a≠0)上存在点C,使得△ABC的紧覆益的边长为3.
当a<0时,抛物线经过点A时,解析式为y=-2(x+1)2,
观察图象可知,当a≤-2时,在抛物线y=ax2+2ax-2(a≠0)上存在点C,使得△ABC的紧覆益的边长为3.
综上所述,满足条件的a的值为a≥![]() 或a≤-2.
或a≤-2.

 阅读快车系列答案
阅读快车系列答案