Question

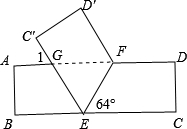将一张矩形纸条ABCD按如图所示折叠，若折叠角∠FEC=64°，∠1=

52

度；△EFG的形状是

等腰三角形

三角形．

Answer 1

分析：根据翻折变换的性质求出∠GEF的度数，从而求出∠GEB的度数，再根据平行线的性质求出∠1；根据AD∥BC得到∠GFE=∠FEC，根据翻折不变性得到∠GEF=∠GFE，由等角对等边得到GE=GF．

解答：（1）解：∵∠GEF=∠FEC=64°，
∴∠BEG=180°-64°×2=52°，
∵AD∥BC，
∴∠1=∠BEG=52°；

（2）证明：∵AD∥BC，
∴∠GFE=∠FEC，
∴∠GEF=∠GFE，
∴GE=GF，
∴△EFG是等腰三角形．
故答案为：52；等腰三角形．

点评：本题考查的是图形翻折变换的性质及等腰三角形的判定定理，熟知图形翻折不变性的性质是解答此题的关键．