题目内容
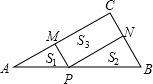如图，Rt△ABC中，∠C=90°，P是斜边AB上的一个动点（不与AB重合），过P分别作PM⊥AC，PN⊥BC，△AMP的面积是S1，△PNB的面积是S2，四边形CMPN的面积是S3，S1+S2与S3之间有怎样的关系？
解：S1+S2与S3之间的关系是S1+S2≥S3．
理由是：（1）当P是AB的中点Q时，过Q做QF⊥BC于F，QE⊥AC于E，连接CQ，
∵∠ACB=90°，
∴QF∥AC，QE∥BC，
∴E为AC的中点，F为BC的中点，
根据等底同高的三角形的面积相等，S△AQE=S△CQE，S△CQF=S△BQF，
∴S△AQE+S△BQF=S△CQE+S△CQF，
即：S1+S2=S3．
（2）当P不是AB的中点Q时，如图：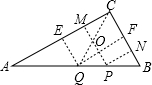
∵QF⊥BC，QE⊥AC，PM⊥AC，PN⊥BC，
∴QE∥PM，PN∥QF，
∴
=
，
=
，
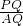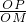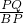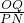∵AQ=BQ＞BP，
∴＜，
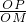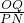即：OP•PN＜OQ•OM，
∴S四边形OPNF＜S四边形OQEM，
∴S四边形CNPM＜S四边形CEQF，
即：S3＜
S△ABC
而S△ABC=S1+S2+S3，
∴S3＜S△ABC=（S1+S2+S3）
∴S3＜S1+S2，
综合上述：S1+S2与S3之间的关系是S1+S2≥S3．
答：S1+S2与S3之间的关系是S1+S2≥S3．
分析：（1）首先假设P是AB的中点时求出S1+S2=S3；（2）当P不是中点时和图形（1）比较利用平行线分线段成比例定理和矩形的面积公式求出S1+S2＞S3，综合（1）（2）即可得出答案．
点评：本题主要考查了面积及等积变换，平行四边形的性质和判定，三角形的面积，平行线分线段成比例定理等知识点，解此题的关键是分类讨论．题目较好，但有一定的难度．
理由是：（1）当P是AB的中点Q时，过Q做QF⊥BC于F，QE⊥AC于E，连接CQ，
∵∠ACB=90°，
∴QF∥AC，QE∥BC，
∴E为AC的中点，F为BC的中点，
根据等底同高的三角形的面积相等，S△AQE=S△CQE，S△CQF=S△BQF，
∴S△AQE+S△BQF=S△CQE+S△CQF，
即：S1+S2=S3．
（2）当P不是AB的中点Q时，如图：
∵QF⊥BC，QE⊥AC，PM⊥AC，PN⊥BC，
∴QE∥PM，PN∥QF，
∴
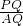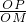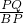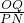=，=，∵AQ=BQ＞BP，
∴
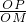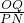＜，即：OP•PN＜OQ•OM，
∴S四边形OPNF＜S四边形OQEM，
∴S四边形CNPM＜S四边形CEQF，
即：S3＜
S△ABC而S△ABC=S1+S2+S3，
∴S3＜
S△ABC=（S1+S2+S3）∴S3＜S1+S2，
综合上述：S1+S2与S3之间的关系是S1+S2≥S3．
答：S1+S2与S3之间的关系是S1+S2≥S3．
分析：（1）首先假设P是AB的中点时求出S1+S2=S3；（2）当P不是中点时和图形（1）比较利用平行线分线段成比例定理和矩形的面积公式求出S1+S2＞S3，综合（1）（2）即可得出答案．
点评：本题主要考查了面积及等积变换，平行四边形的性质和判定，三角形的面积，平行线分线段成比例定理等知识点，解此题的关键是分类讨论．题目较好，但有一定的难度．
练习册系列答案
阅读快车系列答案
相关题目
如图，Rt△ABC中，∠ACB=90°，tanB=
如图，Rt△ABC中，∠C=90°，BC=3，AC=4，若△ABC∽△BDC，则CD=（ ）
如图，Rt△ABC中，∠C=90°，△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F．
如图，Rt△ABC中，∠ABC=90゜，BD⊥AC于D，∠CBD=α，AB=3，BC=4．