��Ŀ����
��ͼ����֪���κ�����ͼ�����O��0��0����A��4��0����B��2���� ����M��OA���е㣮
����M��OA���е㣮
��1����˶��κ����Ľ���ʽ��
��2����P���������ϵ�һ�㣬��P��x���ƽ�����������߽�����һ��Q��Ҫʹ�ı���PQAM�����Σ���P������ꣻ
��3������������x���·��IJ�����x�����Ϸ��ۣ�������OB��A��B��ΪB����x��ĶԳƵ㣩����ԭ������x����Ϸ�����ȡһ��C������CM��CM�뷭�ۺ������OB��A���ڵ�D������CDA������ǡ�MDA�����2���������ĵ�C�Ƿ���ڣ����������C������꣬�������ڣ���˵�����ɣ�
(1) y= x2��
x2�� x��(2) P��1����
x��(2) P��1���� ����(3) ��C��������2+2
����(3) ��C��������2+2 ��
�� ����2��2
����2��2 ��
�� ����
����
���������������1�����ô���ϵ����������κ����Ľ���ʽ��
��2�����ı���PQAM�����Σ���֪PQ=2��PQ��x�ᣬ��˵�P��Q���ڶԳ���x=2�Գƣ��ɵõ�P������Ϊ1���Ӷ������P�����ꣻ
��3������������������ĵ�C���ɡ�CDA������ǡ�MDA�����2�����ɵõ�C�������ǵ�D�������3�����ɴ��з��������C�����꣮
�����������1���������߹�ԭ�㣬���������ʽΪ��y=ax2+bx��
�������߾�����A��4��0����B��2���� ����
����
�� �����
����� ��
��
����κ�������ʽΪ��y= x2��
x2�� x��
x��
��2����y= x2��
x2�� x=
x= ��x��2��2��
��x��2��2�� ��
��
�������߶Գ���Ϊֱ�ߣ�x=2��
���ı���PQAM�����Σ�
��PQ=MA=2��PQ��x�ᣮ
���P��Q���ڶԳ���x=2�Գƣ�
���P������Ϊ1��
��x=1ʱ��y= ��
�� =��
=�� ��
��
��P��1���� ����
����
��3�������⣬����֮��������߽���ʽΪ��y=�� x2+
x2+ x��
x��
������������ĵ�C��
�ߡ�CDA������ǡ�MDA�����2����
��CD=2MD����CM=3MD��
��ͼ��ʾ���ֱ����D��C��x��Ĵ��ߣ�����ֱ�Ϊ��E����F������DE��CF��
�� ��
��
��CF=3DE��MF=3ME��
��C��x�� x2��
x2�� x����
x����
��MF=x��2��ME=MF=��x��2����OE=ME+OM=x+
��D��x+���� ��x+��2+
��x+��2+ ��x+������
��x+������
��CF=3DE��
�� x2��
x2�� x=3[��
x=3[�� ��x+��2+
��x+��2+ ��x+��]��
��x+��]��
�����ã�x2��4x��8=0��
��ã�x1=2+2 ��x2=2��2
��x2=2��2 ��
��
��y1= ��y2=
��y2= ��
��
��������������ĵ�C����C������Ϊ��2+2 ��
�� ����2��2
����2��2 ��
�� ����
����
���㣺���κ����ۺ��⣮

 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д�
 ����ֱ��PN��x���ڵ�N�����������ڵ�B����B���������߶Գ���ĶԳƵ�ΪC������CB��CP��
����ֱ��PN��x���ڵ�N�����������ڵ�B����B���������߶Գ���ĶԳƵ�ΪC������CB��CP��

 ����
���� ��
�� ��
�� ��
�� ���������ϵĶ��㣬
���������ϵĶ��㣬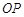 �Ĵ�ֱƽ���߽�
�Ĵ�ֱƽ���߽� ����
���� ��
�� ʱ����
ʱ���� ��
�� �����Ϊ
�����Ϊ ����S����t�ĺ�����ϵʽ�������S�����ֵ��
����S����t�ĺ�����ϵʽ�������S�����ֵ�� ����A����x��ƽ�У�����
����A����x��ƽ�У����� ����
����
 �����㣬���E��x��y������������һ���㣬����x���·����ı���OEBF����OBΪ�Խ��ߵ�ƽ���ı��Σ�
�����㣬���E��x��y������������һ���㣬����x���·����ı���OEBF����OBΪ�Խ��ߵ�ƽ���ı��Σ�


 ��
�� ��m��0��m��
��m��0��m�� ��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ߣ�����y�ύ�ڵ�C����DΪ�����ߵĶ���.
��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ߣ�����y�ύ�ڵ�C����DΪ�����ߵĶ���. DQ�����F������.
DQ�����F������.