题目内容
4. 在△ABC中,CE,BD分别是边AB,AC上的高,F是BC边上的中点.
在△ABC中,CE,BD分别是边AB,AC上的高,F是BC边上的中点.(1)指出图中的一个等腰三角形,并说明理由.
(2)若∠A=x°,求∠EFD的度数(用含x的代数式表达).
(3)猜想∠ABC和∠EDA的数量关系,并证明.
分析 (1)根据直角三角形的性质得到EF=$\frac{1}{2}$BC,DF=$\frac{1}{2}$BC,等量代换即可;
(2)根据三角形内角和定理和等腰三角形的性质计算;
(3)根据圆内接四边形的性质解答.
解答 解:(1)△DEF是等腰三角形.
∵CE,BD分别是边AB,AC上的高,F是BC边上的中点,
∴EF=$\frac{1}{2}$BC,DF=$\frac{1}{2}$BC,
∴EF=DF,
∴△DEF是等腰三角形;
(2)∵FE=FB,FD=FC,
∴∠FEB=∠FBE,∠FDC=∠FCD,
∴∠FEB+∠FDC=∠FBE+∠FCD=180°-∠A=180°-x°,
∠AED+∠ADE=180°-∠A=180°-x°,
∴∠FED+∠FDE=360°-(180°-x°)-(180°-x°)=2x°,
∴∠EFD=180°-2x°;
(3)∠ABC=∠EDA.
∵∠BEC=∠BDC=90°,
∴B、E、D、C四点共圆,
∴∠ABC=∠EDA.
点评 本题考查的是直角三角形的性质、三角形内角和定理、等腰三角形的判定和圆内接四边形的性质,掌握直角三角形中,斜边上的中线等于斜边的一半是解题的关键.

练习册系列答案
相关题目
9.下列运算不正确的是( )
| A. | a3•a2=a5 | B. | (x3)2=x9 | C. | x5+x5=2x5 | D. | (-ab)5÷(-ab)2=-a3b3 |
13.不等式-$\frac{1}{2}$x>-1的解集为( )
| A. | x>2 | B. | x<2 | C. | x>-2 | D. | x<-2 |

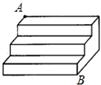 如图是一个三级台阶,它的每一级的长,宽,高分别为100cm,15cm和10cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁想到B点去吃可口的食物,则它所走的最短路线长度为125cm.
如图是一个三级台阶,它的每一级的长,宽,高分别为100cm,15cm和10cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁想到B点去吃可口的食物,则它所走的最短路线长度为125cm.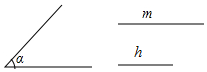 (1)已知∠α和线段m,h,用直尺和圆规作?ABCD,使AB=m,∠DAB=∠α,AB和CD之间的距离为h(作出图形,不写作法,保留痕迹)
(1)已知∠α和线段m,h,用直尺和圆规作?ABCD,使AB=m,∠DAB=∠α,AB和CD之间的距离为h(作出图形,不写作法,保留痕迹)