题目内容
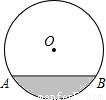
 如图,水平放置的圆柱形排水管的截面半径为12cm,截面中有水部分弓形的高为6cm,则截面中有水部分弓形的面积为________.(结果精确到1cm)
如图,水平放置的圆柱形排水管的截面半径为12cm,截面中有水部分弓形的高为6cm,则截面中有水部分弓形的面积为________.(结果精确到1cm)
88cm2
分析:连接OA、OB,过O作OD⊥AB,交AB于点E,由于弓形的高为6cm可求出OE的长,在Rt△AOE中利用三角函数的定义可求出∠AOE的度数,由垂径定理可知,∠AOE=∠BOE,进而可求出∠AOB的度数,根据扇形及三角形的面积可求出弓形的面积.
解答: 解:连接OA、OB,过O作OD⊥AB,交AB于点E,
解:连接OA、OB,过O作OD⊥AB,交AB于点E,
∵弓形的高为6cm,截面半径为12cm,
∴OE=OD-DE=12-6=6cm,
在Rt△AOE中,OE= OB=6cm,
OB=6cm,
∴AE= =
= =6
=6 ,
,
∴AB=2AE=12
∴∠OAE=30°,∠AOE=60°,
∴∠AOB=2∠AOE=2×60°=120°,
∴S弓形=S扇形AOB-S△AOB= -
- ×12
×12 ×6=
×6= -36
-36 ≈
≈ ×3.14-36×1.73≈88cm2.
×3.14-36×1.73≈88cm2.
故答案为:88cm2.
点评:本题考查的是垂径定理、勾股定理、扇形及三角形的面积,根据题意画出图形是解答此题的关键.
分析:连接OA、OB,过O作OD⊥AB,交AB于点E,由于弓形的高为6cm可求出OE的长,在Rt△AOE中利用三角函数的定义可求出∠AOE的度数,由垂径定理可知,∠AOE=∠BOE,进而可求出∠AOB的度数,根据扇形及三角形的面积可求出弓形的面积.
解答:
 解:连接OA、OB,过O作OD⊥AB,交AB于点E,
解:连接OA、OB,过O作OD⊥AB,交AB于点E,∵弓形的高为6cm,截面半径为12cm,
∴OE=OD-DE=12-6=6cm,
在Rt△AOE中,OE=
 OB=6cm,
OB=6cm,∴AE=
 =
= =6
=6 ,
,∴AB=2AE=12

∴∠OAE=30°,∠AOE=60°,
∴∠AOB=2∠AOE=2×60°=120°,
∴S弓形=S扇形AOB-S△AOB=
 -
- ×12
×12 ×6=
×6= -36
-36 ≈
≈ ×3.14-36×1.73≈88cm2.
×3.14-36×1.73≈88cm2.故答案为:88cm2.
点评:本题考查的是垂径定理、勾股定理、扇形及三角形的面积,根据题意画出图形是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 2、一水平放置的圆柱型水管的横截面如图所示,如果水管横截面的半径是13cm,水面宽AB=24cm,则水管中水深为
2、一水平放置的圆柱型水管的横截面如图所示,如果水管横截面的半径是13cm,水面宽AB=24cm,则水管中水深为 (2012•江门模拟)如图是一个底面水平放置的圆柱,它的左视图是( )
(2012•江门模拟)如图是一个底面水平放置的圆柱,它的左视图是( ) 如图,水平放置的空心圆柱的俯视图是( )
如图,水平放置的空心圆柱的俯视图是( ) 如图,水平放置的空心圆柱的俯视图是
如图,水平放置的空心圆柱的俯视图是