题目内容
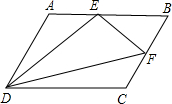
如图，在?ABCD中，E、F分别是边AD、BC的中点，AC分别交BE、DF于G、H，试判断下列结论：①△ABE≌△CDF；②AG=HC；③EG=CH；④S△ABE=S△BDF，其中正确的结论是______．
在?ABCD中，AB=CD，∠BAE=∠DCF，BC=DA；
∵E、F分别是边AD、BC的中点，
∴AE=CF，
在△ABE和△CDF中，
，
∴△ABE≌△CDF（SAS），故①正确；
∵△ABE≌△CDF，
∴∠AEG=∠CFH，
在△AGE和△CHF中，
，
∴△AGE≌△CHF（ASA），
∴AG=HC，故②正确；
若EG=CH，则EG=AG，∠GAE=∠GEA，而这根据题意是无法判断的，故③错误；
∵△ABE与△BFD底相等，高相等，
∴S△ABE=S△BDF，故④正确．
综上可得共有3个结论正确．
故答案为：3．
∵E、F分别是边AD、BC的中点，
∴AE=CF，
在△ABE和△CDF中，
|
∴△ABE≌△CDF（SAS），故①正确；
∵△ABE≌△CDF，
∴∠AEG=∠CFH，
在△AGE和△CHF中，
|
∴△AGE≌△CHF（ASA），
∴AG=HC，故②正确；
若EG=CH，则EG=AG，∠GAE=∠GEA，而这根据题意是无法判断的，故③错误；
∵△ABE与△BFD底相等，高相等，
∴S△ABE=S△BDF，故④正确．
综上可得共有3个结论正确．
故答案为：3．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
