Question

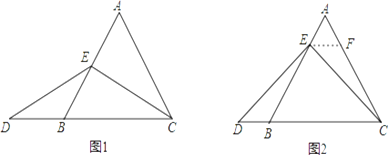
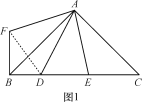
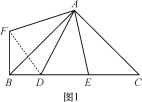
【题目】(1)如图1，△ABC中，∠BAC＝90°，AB＝AC，D，E在BC上，∠DAE＝45°，为了探究BD，DE，CE之间的等量关系，现将△AEC绕A顺时针旋转90°后成△AFB，连接DF，经探究，你所得到的BD，DE，CE之间的等量关系式是 ；(无须证明)

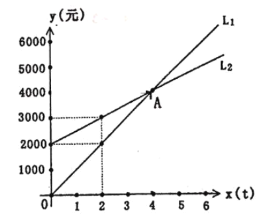
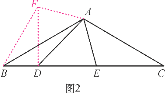
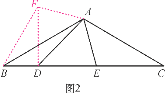
(2)如图2，在△ABC中，∠BAC＝120°，AB＝AC，D，E在BC上，∠DAE＝60°，∠ADE＝45°，试仿照(1)的方法，利用图形的旋转变换，探究BD，DE，CE之间的等量关系，并证明你的结论．

　　　　　　

Answer 1

【答案】(1) BD2＋CE2＝DE2； (2) BD2＋DE2＝CE2，证明见解析.

【解析】

（1）将△AEC绕A顺时针旋转90°后成△AFB，可证△AEC≌△AFB，故BF＝CE，旋转角∠FAE＝90°，又∠DAE＝45°，故∠FAD＝∠FAE∠DAE＝45°，易证△AFD≌△AED，故FD＝DE，因为△ABC中，∠BAC＝90°，AB＝AC，所以∠ABC＝∠FAB＝45°，从而可得∠FAD＝90°，在Rt△FBD中，由勾股定理得线段BD、DE、CE之间的等量关系式；

（2）方法同（1），由∠ADE＝45°可得∠ADF＝45°，故∠BDF＝90°，斜边BF＝CE，直角边DF＝DE，由勾股定理建立等量关系．

(1) BD2＋CE2＝DE2；

(2)CE2＝BD2＋DE2.

证明：将△AEC绕点A顺时针旋转120 °得到△AFB，连接FD.

由旋转的性质可得△AEC≌△AFB，∴AF＝AE，BF＝CE，∠FAB＝∠EAC.

∴∠FAE＝∠FAB＋∠BAE＝∠EAC＋∠BAE＝∠BAC＝120 °.

又∵∠DAE＝60 °，

∴∠FAD＝∠EAD＝60 °.

在△ADF和△ADE中，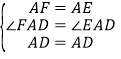

∴△ADF≌△ADE(SAS)．

∴FD＝DE，∠ADF＝∠ADE.

∵∠ADE＝45 °，

∴∠ADF＝45 °，故∠BDF＝90 °.

在Rt△BDF中，由勾股定理，得BF2＝BD2＋DF2.

∴CE2＝BD2＋DE2.