题目内容
如果一个正三角形与一个正六边形的面积相等,那么它们的周长之比是
- A.1:2
- B.
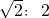
- C.

- D.

C
分析:根据题意画出图形,分别求出正三角形与这个正六边形的面积即可.
解答: 解:设正三角形的边长为2a,正六边形的边长为2b
解:设正三角形的边长为2a,正六边形的边长为2b
(1)过A作AD⊥BC与D,则∠BAD=30°,
AD=AB•cos30°= a,
a,
∴S△ABC= BC•AD=
BC•AD= ×2a×
×2a× a=
a= a2;
a2;
(2)连接OA、OB,过O作OD⊥AB;
∵∠AOB=360°÷6=60°,
∴∠AOD=30°,
OD=ADtan30°= b,
b,
∴S△OAB= ×2b×
×2b× b=
b= b2,
b2,
∴S六边形=6S△OAB=6× b2=6
b2=6 b2,
b2,
∵正三角形与一个正六边形的面积相等,
∴ a2=6
a2=6 b2
b2
∴a:b= :1.
:1.
∴周长之比为 :2,
:2,
故选C.
点评:本题考查了正三角形及正六边形的性质,解答此题的关键是根据题意画出图形,结合正多边形的性质解答.
分析:根据题意画出图形,分别求出正三角形与这个正六边形的面积即可.
解答:
 解:设正三角形的边长为2a,正六边形的边长为2b
解:设正三角形的边长为2a,正六边形的边长为2b(1)过A作AD⊥BC与D,则∠BAD=30°,
AD=AB•cos30°=
 a,
a,∴S△ABC=
 BC•AD=
BC•AD= ×2a×
×2a× a=
a= a2;
a2;(2)连接OA、OB,过O作OD⊥AB;
∵∠AOB=360°÷6=60°,
∴∠AOD=30°,
OD=ADtan30°=
 b,
b,∴S△OAB=
 ×2b×
×2b× b=
b= b2,
b2,∴S六边形=6S△OAB=6×
 b2=6
b2=6 b2,
b2,∵正三角形与一个正六边形的面积相等,
∴
 a2=6
a2=6 b2
b2∴a:b=
 :1.
:1.∴周长之比为
 :2,
:2,故选C.
点评:本题考查了正三角形及正六边形的性质,解答此题的关键是根据题意画出图形,结合正多边形的性质解答.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目




