题目内容
设x*y=xy+2x+2y+2,x,y是任意实数,则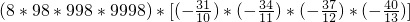 =
=
- A.14×1010-2
- B.14×1010
- C.14×109-2
- D.14×109
C
分析:根据x*y=xy+2x+2y+2=(y+2)(x+2)-2,把式子一步一步展开8*98*998*9998和(- )*(-
)*(-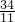 )*(-
)*(-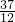 )*(-
)*(-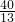 ),再利用新式子计算即可.
),再利用新式子计算即可.
解答:∵x*y=xy+2x+2y+2,
=xy+2x+2y+4-2,
=x(y+2)+2(y+2)-2,
=(y+2)(x+2)-2,
即:x*y=(y+2)(x+2)-2
∴8*98=(8+2)×(98+2)-2=998,
同理998*998=999998,
999998*9998=9 999 999 998,
(- )*(-
)*(-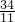 )=-
)=- ,
,
(- )*(-
)*(-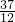 )=-
)=- ,
,
(- )*(-
)*(-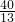 )=-
)=- ,
,
∴原式=9 999 999 998*(- )=(9 999 999 998+2)(-
)=(9 999 999 998+2)(- +2)-2=14×109-2.
+2)-2=14×109-2.
故选C.
点评:本题主要考查了有理数的混合运算,分解因式等知识点,解本题的关键是巧妙地利用式子x*y=xy+2x+2y+2=(y+2)(x+2)-2进行计算,题型较好,规律性好.
分析:根据x*y=xy+2x+2y+2=(y+2)(x+2)-2,把式子一步一步展开8*98*998*9998和(-
 )*(-
)*(-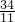 )*(-
)*(-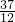 )*(-
)*(-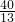 ),再利用新式子计算即可.
),再利用新式子计算即可.解答:∵x*y=xy+2x+2y+2,
=xy+2x+2y+4-2,
=x(y+2)+2(y+2)-2,
=(y+2)(x+2)-2,
即:x*y=(y+2)(x+2)-2
∴8*98=(8+2)×(98+2)-2=998,
同理998*998=999998,
999998*9998=9 999 999 998,
(-
 )*(-
)*(-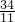 )=-
)=- ,
,(-
 )*(-
)*(-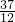 )=-
)=- ,
,(-
 )*(-
)*(-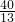 )=-
)=- ,
,∴原式=9 999 999 998*(-
 )=(9 999 999 998+2)(-
)=(9 999 999 998+2)(- +2)-2=14×109-2.
+2)-2=14×109-2.故选C.
点评:本题主要考查了有理数的混合运算,分解因式等知识点,解本题的关键是巧妙地利用式子x*y=xy+2x+2y+2=(y+2)(x+2)-2进行计算,题型较好,规律性好.

练习册系列答案
相关题目
设x*y=xy+2x+2y+2,x,y是任意实数,则(8*98*998*9998)*[(-
)*(-
)*(-
)*(-
)]=( )
| 31 |
| 10 |
| 34 |
| 11 |
| 37 |
| 12 |
| 40 |
| 13 |
| A、14×1010-2 |
| B、14×1010 |
| C、14×109-2 |
| D、14×109 |