题目内容
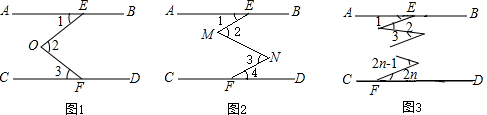
12. 如图,AE∥BF,AC平分∠BAD,交BF于点C,BD平分∠ABC,交AE于点D,连接CD.
如图,AE∥BF,AC平分∠BAD,交BF于点C,BD平分∠ABC,交AE于点D,连接CD.(1)若AB=1,则BC的长=1;
(2)求证:四边形ABCD是菱形.
分析 (1)只要证明△ABC是等腰三角形即可解决问题.
(2)首先证明四边形ABCD是平行四边形,再证明邻边相等即可.
解答 (1)解:∵AC平分∠BAD, ∴∠BAC=∠CAD,
∴∠BAC=∠CAD,
∵AD∥BC,
∴∠DAC=∠BCA,
∴∠BAC=∠BCA,
∴BC=BA=1.
故答案为1.
(2)证明:∵AC平分∠BAD,
∴∠BAC=∠CAD,
∵AD∥BC,
∴∠DAC=∠BCA,
∴∠BAC=∠BCA,
∴BC=BA,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵AD∥BC,
∴∠ADB=∠BDC,
∴∠ABD=∠ADB,
∴AB=AD,
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形,
∵AB=AD,
∴四边形ABCD是菱形.
点评 本题考查菱形的判定、平行四边形的判定和性质、角平分线的性质,等腰三角形的判定等知识,解题的关键是熟练应用这些知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
 、
、 在数轴上的位置,化简
在数轴上的位置,化简  .
.
 如图,点M在∠AOB的边OB上.
如图,点M在∠AOB的边OB上.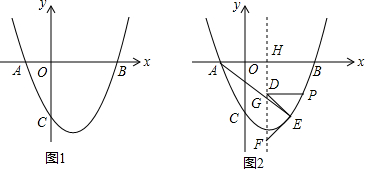 在平面直角坐标中,抛物线y=ax2-3ax-10a(a>0)分别交x轴于点A、B(点A在点B左侧),交y轴于点C,且OB=OC.
在平面直角坐标中,抛物线y=ax2-3ax-10a(a>0)分别交x轴于点A、B(点A在点B左侧),交y轴于点C,且OB=OC. ②
② ③
③ ④
④ 中,一元二次方程的个数是( )
中,一元二次方程的个数是( ) 中,字母x的取值范围是( )
中,字母x的取值范围是( ) B.
B.  C.
C.  D.
D. 
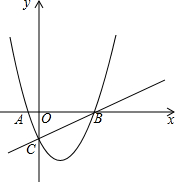 已知:抛物线y=x2+2mx+m,m为常数.
已知:抛物线y=x2+2mx+m,m为常数.