题目内容
3.已知,正比例函数y1=k1x(k1≠0)与反比例函数y2=$\frac{{k}_{2}}{x}$(k2≠0)的图象交于两点,其中一个交点的坐标为(-2,-1),则另一个交点的坐标是( )| A. | (2,1) | B. | (-2,-1) | C. | (-2,1) | D. | (2,-1) |
分析 反比例函数的图象是中心对称图形,则与经过原点的直线的两个交点一定关于原点对称.
解答 解:∵正比例函数y1=k1x(k1≠0)与反比例函数y2=$\frac{{k}_{2}}{x}$(k2≠0)的图象交于两点,正比例函数y1=k1x(k1≠0)与反比例函数y2=$\frac{{k}_{2}}{x}$(k2≠0)的图象均关于原点对称.
则两点关于原点对称,一个交点的坐标为(-2,-1),
则另一个交点的坐标为(2,1).
故选:A.
点评 本题考查了反比例函数与一次函数的交点以及反比例函数图象的中心对称性;熟练掌握反比例函数图象关于原点对称是解决问题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
11.以下调查中,不适宜全面调查的是( )
| A. | 调查某班学生的身高情况 | |
| B. | 调查某批次灯泡的使用寿命 | |
| C. | 调查某舞蹈队成员的鞋码大小 | |
| D. | 调查班级某学习小组成员周末写作业的时间 |
18.2017年3月5日,李克强总理在十二届全国人大五次会议上作政府工作报告谈到,2016年我国国内生产总值达到74.4万亿元,增长6.7%,名列世界前茅.其中74.4万亿元用科学记数法表示为( )
| A. | 7.44×1013元 | B. | 7.44×1012元 | C. | 74.4×1012元 | D. | 7.44×1014元 |
8.在一次引体向上的测试中,小强等5位同学引体向上的次数分别为:6,8,9,8,9,那么关于这组数据的说法正确的是( )
| A. | 平均数是8.5 | B. | 中位数是8.5 | C. | 众数是8.5 | D. | 众数是8和9 |
12.用反证法证明“a<b”,应先假设( )
| A. | a≠b | B. | a>b | C. | a=b | D. | a≥b |
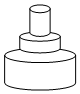 如图,匀速地向该容器内注水,最后把容器注满,在注水过程中容器内液面的高度h随时间t变化的函数图象最接近实际情况的是( )
如图,匀速地向该容器内注水,最后把容器注满,在注水过程中容器内液面的高度h随时间t变化的函数图象最接近实际情况的是( )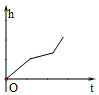
 如图,已知抛物线y=ax2+bx+c经过A(-1,0),B(3,0),C(0,3)三点,直线是抛物线的对称轴.
如图,已知抛物线y=ax2+bx+c经过A(-1,0),B(3,0),C(0,3)三点,直线是抛物线的对称轴.