题目内容
如图,在直角三角形PMN中,∠MPN=90°,PM=PN=6 cm,矩形ABCD的长和宽分别为6 cm和3 cm,C点和P点重合,BC和PN在一条直线上.令Rt△PMN不动,矩形ABCD向右以每秒1 c m的速度移动,直到C点与N点重合为止.设移动x秒后,矩形ABCD与△PMN重合部分的面积为y cm2.
m的速度移动,直到C点与N点重合为止.设移动x秒后,矩形ABCD与△PMN重合部分的面积为y cm2.(1)求y与x之间的函数关系式;
(2)求重合部分面积的最大值.
分析:(1)矩形的右移过程中,它和Rt△PMN之间重叠部分有两种情况:
①当C由P点移动到G点,D点落在MN上的F点的过程中,重叠部分的图形是矩形,此时只要根据矩形的面积公式计算重叠部分的面积即可.根据等腰三角形的性质不难判断出x的取值范围0<x≤3.
②当3<x≤6时,则重叠部分是五边形,这时只要用大三角形的面积减去两个小三角形的面积即可.
(2)根据y与x之间的表达式可直接判断出重合部分面积的最大值.
①当C由P点移动到G点,D点落在MN上的F点的过程中,重叠部分的图形是矩形,此时只要根据矩形的面积公式计算重叠部分的面积即可.根据等腰三角形的性质不难判断出x的取值范围0<x≤3.
②当3<x≤6时,则重叠部分是五边形,这时只要用大三角形的面积减去两个小三角形的面积即可.
(2)根据y与x之间的表达式可直接判断出重合部分面积的最大值.
解答: 解:(1)在矩形的右移过程中,它和Rt△PMN之间重叠部分有两种情况:(1分)
解:(1)在矩形的右移过程中,它和Rt△PMN之间重叠部分有两种情况:(1分)
①如图1,当C由P点移动到G点,D点落在MN上的F点的过程中,重叠部分的图形是矩形,
由于△MPN是等腰Rt△,
所以△MEF也是等腰Rt△.(2分)
PC=x,MP=6,EF=ME=3
∴y=PC•CD=3x(O≤x≤3)(3分)
②如图2,当C是由G点移动到N点的过程中,即3<x≤6时,设CD与MN交于点Q,则重叠部分是五边形EFQCP△NCQ是等腰Rt△(4分)
y=-
(x-6)2+
(3<x≤6)
∴y与x之间的函数关系式为
y=
(2)当x=6时(即c与N重合时),y取得最大值(即重叠部分面积最大),其值为
.
另解:直接由图形知当C与N重合时,该重叠部分面积最大,而此时重叠部分为梯形EPNF,可求得S梯形EPNF=
.
 解:(1)在矩形的右移过程中,它和Rt△PMN之间重叠部分有两种情况:(1分)
解:(1)在矩形的右移过程中,它和Rt△PMN之间重叠部分有两种情况:(1分)①如图1,当C由P点移动到G点,D点落在MN上的F点的过程中,重叠部分的图形是矩形,
由于△MPN是等腰Rt△,
所以△MEF也是等腰Rt△.(2分)
PC=x,MP=6,EF=ME=3
∴y=PC•CD=3x(O≤x≤3)(3分)
②如图2,当C是由G点移动到N点的过程中,即3<x≤6时,设CD与MN交于点Q,则重叠部分是五边形EFQCP△NCQ是等腰Rt△(4分)
y=-
| 1 |
| 2 |
| 27 |
| 2 |
∴y与x之间的函数关系式为
y=
|
(2)当x=6时(即c与N重合时),y取得最大值(即重叠部分面积最大),其值为
| 27 |
| 2 |
另解:直接由图形知当C与N重合时,该重叠部分面积最大,而此时重叠部分为梯形EPNF,可求得S梯形EPNF=
| 27 |
| 2 |
点评:此题比较简单,解答此题的关键是注意矩形在移动过程中的两种情形,根据等腰直角三角形的性质计算x的取值范围.

练习册系列答案
相关题目
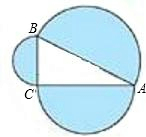 如图,在直角三角形ABC中,∠C=90°,AB=4,阴影部分的面积为( )
如图,在直角三角形ABC中,∠C=90°,AB=4,阴影部分的面积为( )| A、2π | B、3π | C、4π | D、6π |
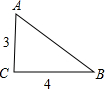
 如图,在直角三角形中,一直角边比另一直角边长1,且斜边长为5.
如图,在直角三角形中,一直角边比另一直角边长1,且斜边长为5.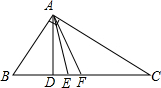 如图,在直角三角形ABC中,AD为斜边上的垂线,AE为角平分线,AF为中线,
如图,在直角三角形ABC中,AD为斜边上的垂线,AE为角平分线,AF为中线, 9、如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,则当AP=
9、如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,则当AP=