题目内容
18.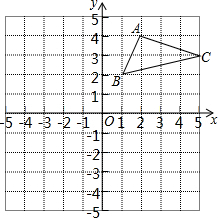 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:(1)画出△ABC关于x轴对称的△A1B1C1,并写出A1的坐标.
(2)求直线BC与y轴的交点D的坐标.
(3)在x轴上有一个动点P,当|PA-PB|的值最大时,点P的坐标为(0,0).
分析 (1)找出A、B、C三点的对称点,再连接即可;
(2)设直线BC的解析式为y=kx+b,根据B、C两点坐标求出BC的解析式,再计算出与y轴的交点坐标即可;
(3)由三角形两边之差小于第三边可知,当A、B、P三点不共线时,|PA-PB|<AB,又因为A(2,4),B(1,2)两点都在x轴同侧,则当A、B、P三点共线时,|PA-PB|=AB,即|PA-PB|≤AB,所以本题中当点P到A、B两点距离之差的绝对值最大时,点P在直线AB上.先运用待定系数法求出直线AB的解析式,再令y=0,求出x的值即可.
解答 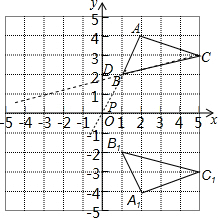 解:(1)如图所示:A1的坐标(2,-4);
解:(1)如图所示:A1的坐标(2,-4);
(2)设直线BC的解析式为y=kx+b,
∵经过B(1,2),C(5,3),
∴$\left\{\begin{array}{l}{2=k+b}\\{3=5k+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{1}{4}}\\{b=\frac{7}{4}}\end{array}\right.$,
∴直线BC的解析式为y=$\frac{1}{4}$x+$\frac{7}{4}$;
当x=0时,y=$\frac{7}{4}$,
∴与y轴的交点D的坐标(0,$\frac{7}{4}$);
(3)当|PA-PB|的值最大时,点P在直线AB上;
设直线AB的解析式为y=mx+a,
∵经过A(2,4),B(1,2),
∴$\left\{\begin{array}{l}{4=2k+b}\\{2=k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=2}\\{b=0}\end{array}\right.$,
∴直线AB的解析式为y=2x,
当y=0时,x=0,
∴P(0,0).
故答案为:(0,0).
点评 此题主要考查了三角形的三边关系定理,运用待定系数法求一次函数的解析式及x轴上点的坐标特征,以及作轴对称图形.根据三角形两边之差小于第三边得出当点P在直线AB上时,P点到A、B两点距离之差的绝对值最大,是解题的关键.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案| A. | 最大的负数 | B. | 最小的非负数 | ||
| C. | 最大的负整数 | D. | 绝对值最小的正整数 |
 如图,菱形ABCD中,AC=16,BD=12,则菱形的周长是( )
如图,菱形ABCD中,AC=16,BD=12,则菱形的周长是( )| A. | 20 | B. | 24 | C. | 28 | D. | 40 |
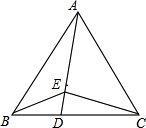 如图,等边△ABC中,D在BC边上,E为AD上一点,若CD=2BD,∠BEC=120°,BE=1,则CE的长度为$\sqrt{2}$.
如图,等边△ABC中,D在BC边上,E为AD上一点,若CD=2BD,∠BEC=120°,BE=1,则CE的长度为$\sqrt{2}$.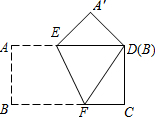 把一张矩形纸片ABCD按如右图方式折叠,使顶点B和顶点D重合,折痕为EF.若∠DEF=60°,FC=2,则BF的长为4.
把一张矩形纸片ABCD按如右图方式折叠,使顶点B和顶点D重合,折痕为EF.若∠DEF=60°,FC=2,则BF的长为4.