题目内容
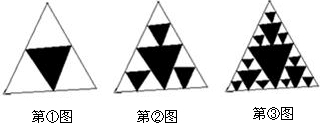
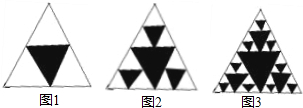
将一个面积为1的等边三角形挖去连接三边中点所组成的三角形(如第①图)后,继续挖去连接剩余各个三角形三边中点所成的三角形(如第②图、第③图)…如此进行挖下去,第④个图中,剩余图形的面积为 ,那么第n(n为正整数)个图中,挖去的所有三角形的面积和为 (用含n的代数式表示).
【答案】分析:观察这几个图,可以看出来,分别在每个图形中,以每个小白三角形为一个基本图形,那么在这个图形中,就会有很多以一个白色三角形为基础的图形,从中发现规律在第N个图形中,会有4n个基本形;也可以看出有3n白色三角形.那么剩余部分的面积为 ×大三角形的面积,然后即可求出挖去的所有三角形的面积和.
×大三角形的面积,然后即可求出挖去的所有三角形的面积和.
解答:解:观察这几个图,可以看出来,分别在每个图形中,以每个小白三角形为一个基本图形,那么在这个图形中,就会有很多以一个白色三角形为基础的图形.则可以观察出规律,在第N个图形中,会有4n个基本形;也可以看出有3n白色三角形.
那么剩余部分的面积就应该是: ×大三角形的面积,即
×大三角形的面积,即 ×大三角形的面积,
×大三角形的面积,
那么第④个图中,剩余图形的面积为 或
或 ,
,
∵三角形的面积是1
第n(n为正整数)个图中,挖去的所有三角形的面积和为:1- .
.
故答案为: 或
或 ;1-
;1- .
.
点评:此题主要考查相似三角形的判定与性质和三角形中位线定理等知识点,解答此题的关键是求出剩余部分的面积为 ×大三角形的面积.然后问题可解.
×大三角形的面积.然后问题可解.
 ×大三角形的面积,然后即可求出挖去的所有三角形的面积和.
×大三角形的面积,然后即可求出挖去的所有三角形的面积和.解答:解:观察这几个图,可以看出来,分别在每个图形中,以每个小白三角形为一个基本图形,那么在这个图形中,就会有很多以一个白色三角形为基础的图形.则可以观察出规律,在第N个图形中,会有4n个基本形;也可以看出有3n白色三角形.
那么剩余部分的面积就应该是:
 ×大三角形的面积,即
×大三角形的面积,即 ×大三角形的面积,
×大三角形的面积,那么第④个图中,剩余图形的面积为
 或
或 ,
,∵三角形的面积是1
第n(n为正整数)个图中,挖去的所有三角形的面积和为:1-
 .
.故答案为:
 或
或 ;1-
;1- .
.点评:此题主要考查相似三角形的判定与性质和三角形中位线定理等知识点,解答此题的关键是求出剩余部分的面积为
 ×大三角形的面积.然后问题可解.
×大三角形的面积.然后问题可解. 
练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目