题目内容
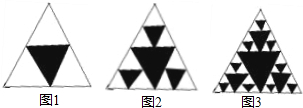
将一个面积为1的等边三角形挖去连接三边中点所组成的三角形(如第①图)后,继续挖去连接剩余各个三角形三边中点所的三角形(如第②图、第③图)…如此进行挖下去,第2010个图形中剩余部分的面积为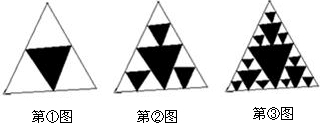
分析:观察这几个图,可以看出来,分别在每个图形中,以每个小白三角形为一个基本图形,那么在这个图形中,就会有很多以一个白色三角形为基础的图形.则可以观察出规律,在第N个图形中,会有4的n次幂个基本形;也可以看出有3的n次幂个白色三角形.那么剩余部分的面积就应该是:4的n次幂分之3的n次幂×大三角形的面积.
解答:解:观察得出规律,在第N个图形中,会有4的n次幂个基本形,
也可以看出有3的n次幂个白色三角形,
那么剩余部分的面积就应该是:4的N次幂分之3的N次幂×大三角形的面积,
根据三角形的面积是1,
那么就可以得出第2010个图形中剩余部分的面积为:4的2010次幂分之3的2010次幂×1
也就是:
×1,
即:(
)2010,
故答案为:(
)2010.
也可以看出有3的n次幂个白色三角形,
那么剩余部分的面积就应该是:4的N次幂分之3的N次幂×大三角形的面积,
根据三角形的面积是1,
那么就可以得出第2010个图形中剩余部分的面积为:4的2010次幂分之3的2010次幂×1
也就是:
| 32010 |
| 42010 |
即:(
| 3 |
| 4 |
故答案为:(
| 3 |
| 4 |
点评:此题考查的知识点是图形的变化类问题,关键是通过观察得到剩余部分的面积就应该是:4的n次幂分之3的n次幂×大三角形的面积.

练习册系列答案
相关题目