Question

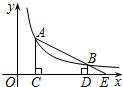如图，A，B是反比例函数y=

2

x

的图象上的两点，AC，BD都垂直于x轴，垂足分别为C，D，AB的延长线交x轴于点E，若C，D的坐标分别为（1，0）、（4，0），则△BDE的面积与△ACE的面积的比值是

 

．

Answer 1

分析：先根据AC，BD都垂直于x轴判断出△BDE∽△ACE，再把C，D两点的横坐标代入反比例函数y=

2

x

即可求出AC、BD的长度，再根据相似三角形的相似比解答即可．

解答：解：∵AC，BD都垂直于x轴，垂足分别为C，D，
∴△BDE∽△ACE，
∵A，B是反比例函数y=

2

x

的图象上的两点，C，D的坐标分别为（1，0）、（4，0），
∴A（1，2），B（4，

1

2

），
∴AC=2，BD=

1

2

，
∴

BD

AC

=

1 2

2

=

1

4

，
∴

S△BDE

S△ACE

=（

BD

AC

）²=

1

16

．

点评：本题考查的是反比例函数图象上点的坐标特点及相似三角形的性质，涉及面较广，但难度适中．