Question

如图，在正方形ABCD中，对角线AC与BD相交于点O，点E是BC上的一个动点，连接DE，交AC于点F．
（1）如图①，当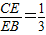时，求的值；
（2）如图②当DE平分∠CDB时，求证：AF=OA；
（3）如图③，当点E是BC的中点时，过点F作FG⊥BC于点G，求证：CG=BG．

Answer 1

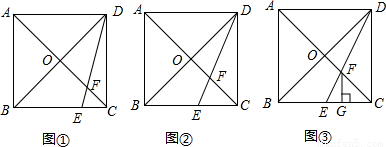
【答案】分析：（1）利用相似三角形的性质求得EF于DF的比值，依据△CEF和△CDF同高，则面积的比就是EF与DF的比值，据此即可求解；
（2）利用三角形的外角和定理证得∠ADF=∠AFD，可以证得AD=AF，在直角△AOD中，利用勾股定理可以证得；
（3）连接OE，易证OE是△BCD的中位线，然后根据△FGC是等腰直角三角形，易证△EGF∽△ECD，利用相似三角形的对应边的比相等即可证得．
解答：（1）解：∵=，
∴=．
∵四边形ABCD是正方形，
∴AD∥BC，AD=BC，
∴△CEF∽△ADF，
∴=，
∴==，
∴==；

（2）证明：∵DE平分∠CDB，∴∠ODF=∠CDF，
又∵AC、BD是正方形ABCD的对角线．
∴∠ADO=∠FCD=45°，∠AOD=90°，OA=OD，而∠ADF=∠ADO+∠ODF，∠AFD=∠FCD+∠CDF，
∴∠ADF=∠AFD，∴AD=AF，
在直角△AOD中，根据勾股定理得：AD==OA，
∴AF=OA．

（3）证明：连接OE．
∵点O是正方形ABCD的对角线AC、BD的交点．
∴点O是BD的中点．
又∵点E是BC的中点，
∴OE是△BCD的中位线，
∴OE∥CD，OE=CD，
∴△OFE∽△CFD．
∴==，
∴=．
又∵FG⊥BC，CD⊥BC，
∴FG∥CD，
∴△EGF∽△ECD，
∴==．
在直角△FGC中，∵∠GCF=45°．
∴CG=GF，
又∵CD=BC，
∴==，
∴=．
∴CG=BG．
点评：本题是勾股定理、三角形的中位线定理、以及相似三角形的判定与性质的综合应用，理解正方形的性质是关键．