题目内容
如图,是某空军部队进行射击训练时在平面直角坐标系中的示意图,在地面O、A两个观测点测得空中固定目标C的仰角分别是α和β,OA=1千米, ,位于O点的正上方
,位于O点的正上方 千米D点处的直升飞机向目标C发射防空导弹,该导弹运行达到距地面最大3千米时,相应水平距离为4千米.(即图中E点)
千米D点处的直升飞机向目标C发射防空导弹,该导弹运行达到距地面最大3千米时,相应水平距离为4千米.(即图中E点)
(1)若导弹运行轨道为一抛物线,求该抛物线的解析式;
(2)按以上轨道运行的导弹能否击中目标C?请说明理由.

解:(1)∵顶点E的坐标为(4,3).
∴设函数的表达式为y=a(x-4)2+3.
将D(0, )代入得,a=-
)代入得,a=- .
.
∴y=- (x-4)2+3
(x-4)2+3
=- x2+
x2+ x+
x+ .
.
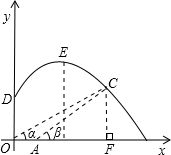
(2)过点C作CF⊥x轴于点F,tanα=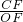 .
.
∵tanα= ,
, =
=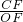 ,
,
∴OF= CF.
CF.
∵tanβ= ,
,
∴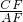 =
= ,∴AF=
,∴AF= CF.
CF.
∵OF-AF=OA=1,
∴ CF-
CF- CF=1,
CF=1,
∴CF= ,OF=
,OF= CF=
CF= ×
× =7,
=7,
∴C(7, ).
).
把x=7代入y=- x2+
x2+ x+
x+ .
.
得y= .
.
∴点C在抛物线上,
∴导弹能击中目标C.
分析:(1)依题意得抛物线顶点E(4,3),经过D(0, ),这顶点式,可求抛物线解析式;
),这顶点式,可求抛物线解析式;
(2)过C点作x轴的垂线,垂足为F,解直角三角形OCF、ACF,可得CF,OF的长,从而可得点C的坐标,判断点C是否满足抛物线解析式.
点评:本题考查点的坐标的求法及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题.
∴设函数的表达式为y=a(x-4)2+3.
将D(0,
 )代入得,a=-
)代入得,a=- .
.∴y=-
 (x-4)2+3
(x-4)2+3=-
 x2+
x2+ x+
x+ .
.
(2)过点C作CF⊥x轴于点F,tanα=
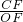 .
.∵tanα=
 ,
, =
=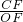 ,
,∴OF=
 CF.
CF.∵tanβ=
 ,
,∴
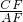 =
= ,∴AF=
,∴AF= CF.
CF.∵OF-AF=OA=1,
∴
 CF-
CF- CF=1,
CF=1,∴CF=
 ,OF=
,OF= CF=
CF= ×
× =7,
=7,∴C(7,
 ).
).把x=7代入y=-
 x2+
x2+ x+
x+ .
.得y=
 .
.∴点C在抛物线上,
∴导弹能击中目标C.
分析:(1)依题意得抛物线顶点E(4,3),经过D(0,
 ),这顶点式,可求抛物线解析式;
),这顶点式,可求抛物线解析式;(2)过C点作x轴的垂线,垂足为F,解直角三角形OCF、ACF,可得CF,OF的长,从而可得点C的坐标,判断点C是否满足抛物线解析式.
点评:本题考查点的坐标的求法及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题.

练习册系列答案
相关题目
 选转后的图形中有多少个等腰直角三角形.
选转后的图形中有多少个等腰直角三角形.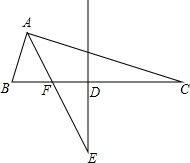 如图,△ABC中,∠BAC=90°,BC的垂直平分线和BC相交于点D,和∠BAC的平分线AE相交于点E,AE和BC相交于点F.求证:DE=
如图,△ABC中,∠BAC=90°,BC的垂直平分线和BC相交于点D,和∠BAC的平分线AE相交于点E,AE和BC相交于点F.求证:DE= BC.
BC. 如图,△ABC中,BD平分∠ABC,DE∥BC交AB于点E,EF∥AC交BC于F,试说明BE=CF.
如图,△ABC中,BD平分∠ABC,DE∥BC交AB于点E,EF∥AC交BC于F,试说明BE=CF. ;
; (
( .
.
 如图,作出△ABC中AC边上的高,∠ABC的角平分线,BC边上的中线.
如图,作出△ABC中AC边上的高,∠ABC的角平分线,BC边上的中线.