题目内容
某商店按批发价每件6元购进一批货,零售价为8元时可卖出100件,如果零售价高于8元则一件也卖不出去,如果零售价从8元每减低0.1元则可以多卖出100件.
(1)写出可卖出的件数q与零售价x(6<x≤8)之间的函数关系式;
(2)这时所获利润y(元)与零售价x(6<x≤8)之间的函数关系式?
(3)试求零售价定为多少时,所获利润最大?最大利润是多少?
(1)写出可卖出的件数q与零售价x(6<x≤8)之间的函数关系式;
(2)这时所获利润y(元)与零售价x(6<x≤8)之间的函数关系式?
(3)试求零售价定为多少时,所获利润最大?最大利润是多少?
考点:二次函数的应用
专题:
分析:(1)100+多卖的件数,进而得出q与零售价x(6<x≤8)之间的函数关系式;
(2)利润=销售量×每件利润,进而得出利润y(元)与零售价x(6<x≤8)之间的函数关系式;
(3)运用函数性质求解结合公式求出即可.
(2)利润=销售量×每件利润,进而得出利润y(元)与零售价x(6<x≤8)之间的函数关系式;
(3)运用函数性质求解结合公式求出即可.
解答:解:(1)由题意可得:q=100+(8-x)÷0.1×10=100+100(8-x)=-100x+900;
(2)根据题意可得:y=(x-6)(900-100x),
即y=-100x2+1500x-5400;
(3)∵-100<0,
∴函数y有最大值.
当x=-
=7.5元时,y最大=
=225(元),
即当零售价定为7.5元时,所获利润最大,最大利润是225元.
(2)根据题意可得:y=(x-6)(900-100x),
即y=-100x2+1500x-5400;
(3)∵-100<0,
∴函数y有最大值.
当x=-
| 1500 |
| 2×(-100) |
| 4×(-100)×(-5400)-15002 |
| 4×(-100) |
即当零售价定为7.5元时,所获利润最大,最大利润是225元.
点评:本题考查了二次函数的应用.此题问题层层推进,为确定最大利润方案做铺垫.运用二次函数求最值,常用方法是公式法和配方法.

练习册系列答案
相关题目
 如图,在△ABC中,点D是AC上一点,添加下列哪个条件不能得到△CBD∽△CAB的是( )
如图,在△ABC中,点D是AC上一点,添加下列哪个条件不能得到△CBD∽△CAB的是( )| A、∠CDB=∠CBA |
| B、∠CBD=∠A |
| C、BC•AB=BD•AC |
| D、BC2=CD•AC |
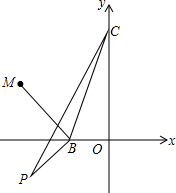 如图,已知,B(-1,0)、C(0,3)、P(-2,-1),M(-2.5,1.5),若点N在坐标平面内,满足△BMN∽△BPC,请直接写出所有符合条件的点N的坐标.
如图,已知,B(-1,0)、C(0,3)、P(-2,-1),M(-2.5,1.5),若点N在坐标平面内,满足△BMN∽△BPC,请直接写出所有符合条件的点N的坐标. 如图,BCD是一条直线,∠1=∠B,∠2=∠A,指出∠1的同位角,∠2的内错角,并求出∠A+∠B+∠ACB的度数.
如图,BCD是一条直线,∠1=∠B,∠2=∠A,指出∠1的同位角,∠2的内错角,并求出∠A+∠B+∠ACB的度数.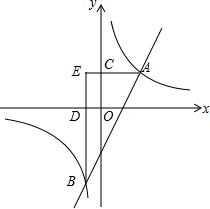 如图,双曲线y=
如图,双曲线y=