题目内容
10．
如图：阴影部分（阴影部分为正方形）的面积是25．
分析 由勾股定理即可得出阴影部分（阴影部分为正方形）的面积．
解答 解：根据题意，由勾股定理得：
阴影部分（阴影部分为正方形）的面积=132-122=25；
故答案为：25．
点评 本题考查了正方形的性质、勾股定理；熟练掌握正方形面积的计算方法，由勾股定理得出结果是解决问题的关键．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
1．关于x的方程-ax=b（a≠0）的解是（ ）
| A． | x=$\frac{b}{a}$ | B． | x=-$\frac{b}{a}$ | C． | x=-$\frac{a}{b}$ | D． | x=$\frac{a}{b}$ |
18．式子（x-3）0+$\sqrt{x}$有意义，则x的取值范围是（ ）
| A． | x≠3 | B． | x≥0 | C． | x≠3或x≥0 | D． | x≠3且x≥0 |
15．
如图，一块直角边分别为6cm和8cm的三角形木板，绕6cm的边旋转一周，则斜边扫过的面积是（ ）
如图，一块直角边分别为6cm和8cm的三角形木板，绕6cm的边旋转一周，则斜边扫过的面积是（ ）| A． | 48πcm2 | B． | 60πcm2 | C． | 80πcm2 | D． | 90πcm2 |
2．
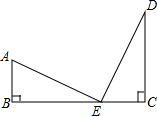如图所示，Rt△ABE≌Rt△ECD，点B、E、C在同一直线上，则结论：①AE=ED；②AE⊥DE；③BC=AB+CD；④AB∥DC中成立的是（ ）
如图所示，Rt△ABE≌Rt△ECD，点B、E、C在同一直线上，则结论：①AE=ED；②AE⊥DE；③BC=AB+CD；④AB∥DC中成立的是（ ）| A． | 仅① | B． | 仅①③ | C． | 仅①③④ | D． | 仅①②③④ |
19．如果2a+b=0（a≠0），则|$\frac{a}{|b|}$-1|+|$\frac{|a|}{b}$-2|的值为（ ）
| A． | 1或2 | B． | 2或3 | C． | 3 | D． | 4 |