题目内容
D，E分别是△ABC中边AB，AC上的点，若DE∥BC，且S△ADE=S梯形DBCE，则AD：DB=
- A.1：1
- B.1：
- C.
- D.
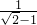
D
分析：根据S△ADE=S梯形DBCE根据三角形面积计算公式即可求得AD与AB的比值，令AD=1，即可求得DB的值，即可解题．
解答：
解：∵S△ADE=S梯形DBCE，
∴△ADE的面积是△ABC面积的一半，
∴
•
=
，
∴AB=AD，
令AD=1，则DB=-1，
∴AD：DB=．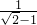
故选D．
点评：本题考查了三角形面积的计算公式，相似三角形对应边比值相等的性质，本题中计算相似三角形的相似比是解题的关键．
分析：根据S△ADE=S梯形DBCE根据三角形面积计算公式即可求得AD与AB的比值，令AD=1，即可求得DB的值，即可解题．
解答：
解：∵S△ADE=S梯形DBCE，∴△ADE的面积是△ABC面积的一半，
∴
•=，∴AB=
AD，令AD=1，则DB=
-1，∴AD：DB=
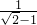．故选D．
点评：本题考查了三角形面积的计算公式，相似三角形对应边比值相等的性质，本题中计算相似三角形的相似比是解题的关键．
练习册系列答案
相关题目
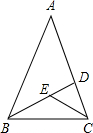如图，在△ABC中，AB=AC，∠A=36°，BD、CE分别是∠ABC、∠BCD的角平分线，则图中的等腰三角形有（ ）| A、5个 | B、4个 | C、3个 | D、2个 |
如图所示，已知点E、F分别是△ABC中AC、AB边的中点，BE、CF相交于点G，FG=1，则CF的长为（ ）| A、2 | B、1.5 | C、3 | D、4 |
16、如图，D，E分别是△ABC的边CA、BA的延长线上的点，请你添加一个条件，使△ADE与△ABC相似．你添加的条件是
如图，点D，E，F分别是△ABC（AB＞AC）各边中点，下列说法不正确的是（ ）
如图，在六边形ABCDEF中，BA⊥FA，BC⊥DC，∠α、∠β分别是∠ABC和∠EDC的补角，∠α=55°，∠β=30°，则∠E+∠F的度数为