题目内容
 如图,在六边形ABCDEF中,BA⊥FA,BC⊥DC,∠α、∠β分别是∠ABC和∠EDC的补角,∠α=55°,∠β=30°,则∠E+∠F的度数为
如图,在六边形ABCDEF中,BA⊥FA,BC⊥DC,∠α、∠β分别是∠ABC和∠EDC的补角,∠α=55°,∠β=30°,则∠E+∠F的度数为265°
265°
.分析:首先根据垂直定义可得∠A=90°,∠C=90°,再由∠α=55°、∠β=30°,可得∠EDC=150°,∠ABC=125°,再利用多边形内角和计算出∠E+∠F的度数即可.
解答:解:∵BA⊥FA,BC⊥DC,
∴∠A=90°,∠C=90°,
∵∠α=55°、∠β=30°,
∴∠EDC=150°,∠ABC=125°,
∴∠E+∠F=180°(6-2)-150°-125°-90°-90°=265°,
故答案为:265°.
∴∠A=90°,∠C=90°,
∵∠α=55°、∠β=30°,
∴∠EDC=150°,∠ABC=125°,
∴∠E+∠F=180°(6-2)-150°-125°-90°-90°=265°,
故答案为:265°.
点评:此题主要考查了多边形内角和,关键是掌握多边形内角和公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
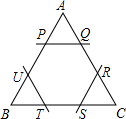 如图所示,△ABC是边长为a的正三角形纸张,今在各角剪去一个三角形,使得剩下的六边形PQRSTU为正六边形,则此正六边形的周长为何( )
如图所示,△ABC是边长为a的正三角形纸张,今在各角剪去一个三角形,使得剩下的六边形PQRSTU为正六边形,则此正六边形的周长为何( )| A、2a | ||
| B、3a | ||
C、
| ||
D、
|
 23、如图,在六边形ABCDEF中,AB=BC=CD=DE=EF=FA,∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA,对角线AE与BF相交于点M,BD与CE相交于点N.
23、如图,在六边形ABCDEF中,AB=BC=CD=DE=EF=FA,∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA,对角线AE与BF相交于点M,BD与CE相交于点N.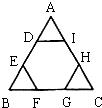 18、如图,正六边形DEFGHI的顶点都在边长为6cm的正三角形ABC的边上,则这个正六边形的边长是
18、如图,正六边形DEFGHI的顶点都在边长为6cm的正三角形ABC的边上,则这个正六边形的边长是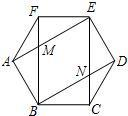 如图,在六边形ABCDEF中,AB=BC=CD=DE=EF=FA,∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA,对角线AE与BF相交于点M,BD与CE相交于点N.
如图,在六边形ABCDEF中,AB=BC=CD=DE=EF=FA,∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA,对角线AE与BF相交于点M,BD与CE相交于点N.