题目内容
如图所示,AB∥CD,分别探讨下面图形中∠AEC,∠EAB,∠ECD的关系.

(1)如图①,求∠AEC+∠EAB+∠ECD的度数.
(2)请你猜想图②中三个角之间的关系;
(3)在图③中,∠AEC-∠EAB+∠ECD=180°,请验证.
解:(1)∠AEC+∠EAB+∠ECD=360°,
过点E作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠BAE+∠1=180°,∠2+∠ECD=180°,
∴∠BAE+∠1+∠2+∠ECD=360°,
∴∠AEC+∠EAB+∠ECD=360°;

(2)∠AEC=∠BAE+∠ECD,
过点E作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠1=∠BAE,∠2=∠ECD,
∴∠AEC=∠1+∠2=∠BAE+∠ECD;
(3)证明:如图3,过点E作PE∥AB,
∵AB∥CD,
∴AB∥CD∥PE,
∴∠1=∠BAE,∠2+∠ECD=180°,
∴∠AEC-∠1+∠ECD=180°,即∠AEC-∠EAB+∠ECD=180°.
分析:(1)先过点E作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,同旁内角互补,即可求得答案;
(2)先过点E作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,内错角相等,即可求得答案;
(3)过点E作PE∥AB,由平行线的性质可得出AB∥CD∥PE,∠1=∠BAE,∠2+∠ECD=180°,故∠AEC-∠1+∠ECD=180°,即∠AEC-∠EAB+∠ECD=180°.
点评:本题考查的是平行线的性质,根据题意作出辅助线,构造出平行线是解答此题的关键.
过点E作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠BAE+∠1=180°,∠2+∠ECD=180°,
∴∠BAE+∠1+∠2+∠ECD=360°,
∴∠AEC+∠EAB+∠ECD=360°;

(2)∠AEC=∠BAE+∠ECD,
过点E作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠1=∠BAE,∠2=∠ECD,
∴∠AEC=∠1+∠2=∠BAE+∠ECD;
(3)证明:如图3,过点E作PE∥AB,
∵AB∥CD,
∴AB∥CD∥PE,
∴∠1=∠BAE,∠2+∠ECD=180°,
∴∠AEC-∠1+∠ECD=180°,即∠AEC-∠EAB+∠ECD=180°.
分析:(1)先过点E作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,同旁内角互补,即可求得答案;
(2)先过点E作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,内错角相等,即可求得答案;
(3)过点E作PE∥AB,由平行线的性质可得出AB∥CD∥PE,∠1=∠BAE,∠2+∠ECD=180°,故∠AEC-∠1+∠ECD=180°,即∠AEC-∠EAB+∠ECD=180°.
点评:本题考查的是平行线的性质,根据题意作出辅助线,构造出平行线是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 5、如图所示,AB∥CD,则∠1+∠2+∠3=( )
5、如图所示,AB∥CD,则∠1+∠2+∠3=( )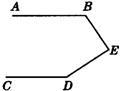 24、已知:如图所示,AB∥CD,若∠ABE=130°,∠CDE=152°,则∠BED=
24、已知:如图所示,AB∥CD,若∠ABE=130°,∠CDE=152°,则∠BED=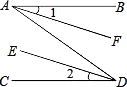 如图所示,AB∥CD,需增加什么条件才能使∠1=∠2成立?
如图所示,AB∥CD,需增加什么条件才能使∠1=∠2成立?
 如图所示,AB∥CD,EG⊥AB,垂足为G,若∠1=42°,则∠E=
如图所示,AB∥CD,EG⊥AB,垂足为G,若∠1=42°,则∠E=