题目内容
19. 如图,∠ABD=∠ACD=90°,∠CBD=∠BCD,则AD平分∠BAC,请说明理由.
如图,∠ABD=∠ACD=90°,∠CBD=∠BCD,则AD平分∠BAC,请说明理由.
分析 AD平分∠BAC,理由为:由已知角相等,利用等角对等边得到BD=CD,再由AD=AD,利用HL得到直角三角形ABD与直角三角形ACD全等,利用全等三角形对应角相等即可得证.
解答 解:AD平分∠BAC,理由为:
∵∠CBD=∠BCD,
∴BD=CD,
在Rt△ABD和Rt△ACD中,
$\left\{\begin{array}{l}{AD=AD}\\{BD=CD}\end{array}\right.$,
∴Rt△ABD≌Rt△ACD(HL),
∴∠BAD=∠CAD,
则AD平分∠BAC.
点评 此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.在下列抽样调查中,你认为选取的样本具有代表性的是( )
| A. | 为了解某地区居民的防火意识,对该地区的初中生进行调查 | |
| B. | 为了解某商场的平均日营业额,选在周末进行调查 | |
| C. | 为了解某校1200名学生的视力情况,随机抽取该校120名学生进行调查 | |
| D. | 为了解全校学生课外小组的活动情况,对该校的男生进行调查 |
9.若(x+2y)2+|x+y+3|=0,则满足该等式的x,y的值分别是( )
| A. | x=3,y=-6 | B. | x=-6,y=3 | C. | x=3,y=6 | D. | x=-3,y=-6 |
 (1)如图,∠ABC与∠EAD是直线AD和直线BC被直线BE所截形成的同位角,∠ABC与∠BCD是直线AB和直线CD被直线BC所截形成的同旁内角
(1)如图,∠ABC与∠EAD是直线AD和直线BC被直线BE所截形成的同位角,∠ABC与∠BCD是直线AB和直线CD被直线BC所截形成的同旁内角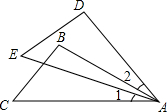 如图,△ABC≌△ADE,∠1=30°,则∠2=30°.
如图,△ABC≌△ADE,∠1=30°,则∠2=30°.