题目内容
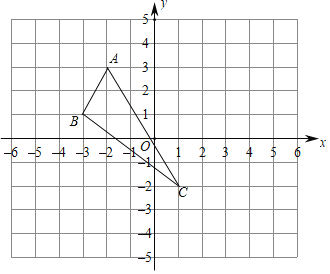
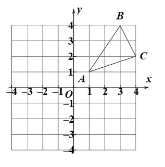
【题目】如图，在平面直角坐标系中，
的三个顶点坐标分别为
，
，
．
（1）在图中画出关于
轴对称的
；
（2）通过平移，使
移动到原点
的位置，画出平移后的
．
（3）在中有一点
，则经过以上两次变换后点
的对应点
的坐标为 ．
【答案】（1）图见解析；（2）图见解析；（3）
【解析】
（1）先分别找到A、B、C关于x轴的对称点
，然后连接
、
、
即可；
（2）先判断
移动到原点
的位置时的平移规律，然后分别将
、按此规律平移，得到
、
,连接
、
、
即可；
（3）根据关于x轴对称的两点坐标关系：横坐标相同，纵坐标互为相反数即可得到
，然后根据（2）中的平移规律即可得到
的坐标．
解：（1）先分别找到A、B、C关于x轴的对称点，然后连接、、，如下图所示：
即为所求
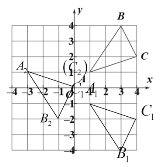
（2）∵
∴
∴到点O（0,0）的平移规律为：先向左平移4个单位，再向上平移2个单位
分别将、按此规律平移，得到、,连接、、，如图所示，
即为所求；
（3）由（1）可知，
经过第一次变化后为
然后根据（2）的平移规律，经过第二次变化后为
故答案为：．
练习册系列答案
相关题目
