题目内容
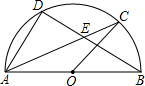 (2003•河南)如图,点D、C是以AB为直径的半圆上的两点,O为圆心,DE与AC相交于点E,OC∥AD,AB=5,cos∠CAB=0.8,求CE和DE的长.
(2003•河南)如图,点D、C是以AB为直径的半圆上的两点,O为圆心,DE与AC相交于点E,OC∥AD,AB=5,cos∠CAB=0.8,求CE和DE的长.分析:OC交BD于F点,连结BC,根据圆周角定理由AB为直径得∠D=90°,∠ACB=90°,在Rt△ABC中可解得AC=4,BC=3,由OC∥AD,则∠OFB=90°,即OF⊥DB,根据垂径定理得DC弧=BC弧,DF=BF,则∠CBD=∠CAB,再在Rt△CBF中,解直角三角形得BF=2.4,CF=1.8,在Rt△CEF中解得EC=
,EF=
,然后利用DE+EF=BF计算出DE.
| 9 |
| 4 |
| 27 |
| 20 |
解答:解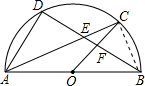 :OC交BD于F点,连结BC,如图,
:OC交BD于F点,连结BC,如图,
∵AB为直径,
∴∠D=90°,∠ACB=90°,
∵cos∠CAB=
=0.8,AB=5,
∴AC=4,
∴BC=
=3,
∵OC∥AD,
∴∠OFB=90°,即OF⊥DB,
∴DC弧=BC弧,DF=BF,
∴∠CBD=∠CAB,
在Rt△CBF中,cos∠CBF=0.8=
,则BF=2.4,
∴CF=
=1.8,
在Rt△CEF中,∠ECF=∠CAB,
∴cos∠ECF=0.8=
,
∴EC=
=
,
∴EF=
=
,
∵DE+EF=BF,
∴DE=2.4-
=1.05.
 :OC交BD于F点,连结BC,如图,
:OC交BD于F点,连结BC,如图,∵AB为直径,
∴∠D=90°,∠ACB=90°,
∵cos∠CAB=
| AC |
| AB |
∴AC=4,
∴BC=
| AB2-AC2 |
∵OC∥AD,
∴∠OFB=90°,即OF⊥DB,
∴DC弧=BC弧,DF=BF,
∴∠CBD=∠CAB,
在Rt△CBF中,cos∠CBF=0.8=
| BF |
| BC |
∴CF=
| BC2-BF2 |
在Rt△CEF中,∠ECF=∠CAB,
∴cos∠ECF=0.8=
| CF |
| EC |
∴EC=
| 1.8 |
| 0.8 |
| 9 |
| 4 |
∴EF=
| EC2-CF2 |
| 27 |
| 20 |
∵DE+EF=BF,
∴DE=2.4-
| 27 |
| 20 |
点评:本题考查了圆周角定理及其讨论:在同圆或等圆中,同弧或等弧所对的圆周角相等;直径所对的圆周角为直角.也考查了垂径定理和勾股定理以及解直角三角形.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
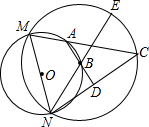 (2003•河南)如图,⊙O、⊙B相交于点M、N,点B在⊙O上,NE为⊙B的直径,点C在⊙B上,CM交⊙O于点A,连接AB并延长交NC于点D,求证:AD⊥NC.
(2003•河南)如图,⊙O、⊙B相交于点M、N,点B在⊙O上,NE为⊙B的直径,点C在⊙B上,CM交⊙O于点A,连接AB并延长交NC于点D,求证:AD⊥NC.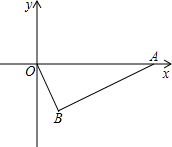 (2003•河南)如图,Rt△OAB的斜边AO在x轴的正半轴上,直角顶点B在第四象限内,S△OAB=20,OB:AB=1:2,求A、B两点的坐标.
(2003•河南)如图,Rt△OAB的斜边AO在x轴的正半轴上,直角顶点B在第四象限内,S△OAB=20,OB:AB=1:2,求A、B两点的坐标.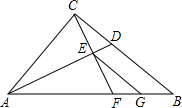 (2003•河南)如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB交BC于点D,过点C作CE⊥AD于E,CE的延长线交AB于点F,过点E作EG∥BC交AB于点G,AE•AD=16,AB=4
(2003•河南)如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB交BC于点D,过点C作CE⊥AD于E,CE的延长线交AB于点F,过点E作EG∥BC交AB于点G,AE•AD=16,AB=4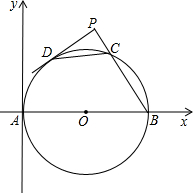 (2003•河南)如图,AB是⊙O的直径,O为圆心,AB=20,DP与⊙O相切于点D,DP⊥PB,垂足为P,PB与⊙O交于点C,PD=8.
(2003•河南)如图,AB是⊙O的直径,O为圆心,AB=20,DP与⊙O相切于点D,DP⊥PB,垂足为P,PB与⊙O交于点C,PD=8.