题目内容
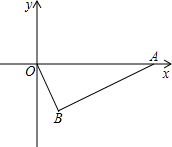 (2003•河南)如图,Rt△OAB的斜边AO在x轴的正半轴上,直角顶点B在第四象限内,S△OAB=20,OB:AB=1:2,求A、B两点的坐标.
(2003•河南)如图,Rt△OAB的斜边AO在x轴的正半轴上,直角顶点B在第四象限内,S△OAB=20,OB:AB=1:2,求A、B两点的坐标.分析:因为OB:AB=1:2,∠OBA为直角,可设OB=x,则AB=2x,OA=
x,因为S△OAB=20=
OB•AB,从而求出x的值,进而得到A点的坐标,过点B作BC⊥OA交OA于C,利用三角形OBA的面积求出OA边上的高,利用勾股定理再求出OC的长即可求出B的坐标.
| 5 |
| 1 |
| 2 |
解答:解:∵OB:AB=1:2,
∴设OB=x,则AB=2x,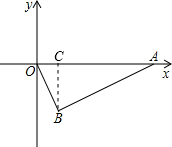
∴OA=
=
x,
∵S△OAB=20=
OB•AB,
∴20=
•x•2x,
∴x2=20,
∴x=2
,
∴OA=
×2
=10,
∴点A的坐标是(10,0);
过点B作BC⊥OA交OA于C,
∵S△AOB=
AO•BC=20,
∴BC=4,
∵B在第四象限,
∴B的纵坐标为-4,
∵OB=2
,BC=4,
∴OC=
=2,
∴B的横坐标是2,
∴B的坐标为(2,-4).
∴设OB=x,则AB=2x,

∴OA=
| OB2+AB2 |
| 5 |
∵S△OAB=20=
| 1 |
| 2 |
∴20=
| 1 |
| 2 |
∴x2=20,
∴x=2
| 5 |
∴OA=
| 5 |
| 5 |
∴点A的坐标是(10,0);
过点B作BC⊥OA交OA于C,
∵S△AOB=
| 1 |
| 2 |
∴BC=4,
∵B在第四象限,
∴B的纵坐标为-4,
∵OB=2
| 5 |
∴OC=
| OB2-BC2 |
∴B的横坐标是2,
∴B的坐标为(2,-4).
点评:本题考查了直角三角形的面积公式、勾股定理的运用以及求点的坐标,题目难度不大,但设计比较新颖.

练习册系列答案
相关题目
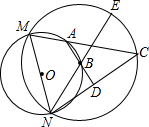 (2003•河南)如图,⊙O、⊙B相交于点M、N,点B在⊙O上,NE为⊙B的直径,点C在⊙B上,CM交⊙O于点A,连接AB并延长交NC于点D,求证:AD⊥NC.
(2003•河南)如图,⊙O、⊙B相交于点M、N,点B在⊙O上,NE为⊙B的直径,点C在⊙B上,CM交⊙O于点A,连接AB并延长交NC于点D,求证:AD⊥NC.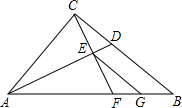 (2003•河南)如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB交BC于点D,过点C作CE⊥AD于E,CE的延长线交AB于点F,过点E作EG∥BC交AB于点G,AE•AD=16,AB=4
(2003•河南)如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB交BC于点D,过点C作CE⊥AD于E,CE的延长线交AB于点F,过点E作EG∥BC交AB于点G,AE•AD=16,AB=4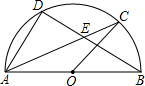 (2003•河南)如图,点D、C是以AB为直径的半圆上的两点,O为圆心,DE与AC相交于点E,OC∥AD,AB=5,cos∠CAB=0.8,求CE和DE的长.
(2003•河南)如图,点D、C是以AB为直径的半圆上的两点,O为圆心,DE与AC相交于点E,OC∥AD,AB=5,cos∠CAB=0.8,求CE和DE的长.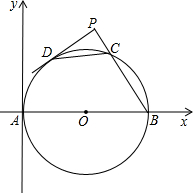 (2003•河南)如图,AB是⊙O的直径,O为圆心,AB=20,DP与⊙O相切于点D,DP⊥PB,垂足为P,PB与⊙O交于点C,PD=8.
(2003•河南)如图,AB是⊙O的直径,O为圆心,AB=20,DP与⊙O相切于点D,DP⊥PB,垂足为P,PB与⊙O交于点C,PD=8.