题目内容
已知椭圆方程为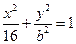
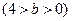 ,P为椭圆上的动点,F1、F2为椭圆的两焦点,当点P不在x轴上时,过F1作∠F1PF2的外角平分线的垂线F1M,垂足为M,当点P在x轴上时,定义M与P重合.
,P为椭圆上的动点,F1、F2为椭圆的两焦点,当点P不在x轴上时,过F1作∠F1PF2的外角平分线的垂线F1M,垂足为M,当点P在x轴上时,定义M与P重合.(Ⅰ)求M点的轨迹T的方程;
(Ⅱ)已知
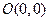 、
、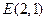 ,试探究是否存在这样的点
,试探究是否存在这样的点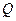 :
: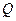 是轨迹T内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积
是轨迹T内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积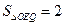 ?若存在,求出点Q的坐标,若不存在,说明理由.
?若存在,求出点Q的坐标,若不存在,说明理由.
解:(Ⅰ)当点P不在x轴上时,延长F1M与F2P的延长线相交于点N,连结OM,

∵ ,
, ∴
∴ ≌
≌ ∴M是线段
∴M是线段 的中点,
的中点, |,
|,
∴ =
=
 =
= =
=
∵点P在椭圆上
∴ =
= ∴
∴ =4,
=4,
当点P在x轴上时,M与P重合
∴M点的轨迹T的方程为: .
.
(Ⅱ)连结OE,易知轨迹T上有两个点

A ,B
,B 满足
满足 ,
,
分别过A、B作直线OE的两条平行线 、
、 .
.
∵同底等高的两个三角形的面积相等
∴符合条件的点均在直线 、
、 上.
上.
∵ ∴直线
∴直线 、
、 的方程分别为:
的方程分别为:
 、
、
设点 (
( )∵
)∵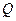 在轨迹T内,∴
在轨迹T内,∴
分别解 与
与 ,得
,得 与
与
∵ ∴
∴ 为偶数,在
为偶数,在 上
上 对应的
对应的
在 上
上 ,对应的
,对应的
∴满足条件的点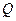 存在,共有6个,它们的坐标分别为:
存在,共有6个,它们的坐标分别为:

 .解析:
.解析:
略

∵
 ,
, ∴
∴ ≌
≌ ∴M是线段
∴M是线段 的中点,
的中点, |,
|,∴
 =
=
 =
= =
=
∵点P在椭圆上
∴
 =
= ∴
∴ =4,
=4,当点P在x轴上时,M与P重合
∴M点的轨迹T的方程为:
 .
.(Ⅱ)连结OE,易知轨迹T上有两个点

A
 ,B
,B 满足
满足 ,
,分别过A、B作直线OE的两条平行线
 、
、 .
. ∵同底等高的两个三角形的面积相等
∴符合条件的点均在直线
 、
、 上.
上.∵
 ∴直线
∴直线 、
、 的方程分别为:
的方程分别为: 、
、
设点
 (
( )∵
)∵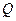 在轨迹T内,∴
在轨迹T内,∴
分别解
 与
与 ,得
,得 与
与
∵
 ∴
∴ 为偶数,在
为偶数,在 上
上 对应的
对应的
在
 上
上 ,对应的
,对应的
∴满足条件的点
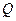 存在,共有6个,它们的坐标分别为:
存在,共有6个,它们的坐标分别为:
 .解析:
.解析:略

练习册系列答案
相关题目
 的椭圆
的椭圆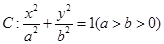 过点M(2,1),O为坐标原点,平行于OM的直线
过点M(2,1),O为坐标原点,平行于OM的直线 交椭圆C于不同的两点A、B。
交椭圆C于不同的两点A、B。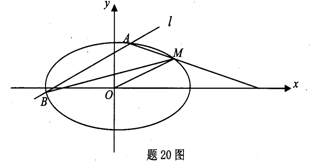
 (a>b>0)的左、右焦点分别为
(a>b>0)的左、右焦点分别为 ,短轴两个端点为.A、B且四边形
,短轴两个端点为.A、B且四边形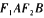 是边长为2的正方形.
是边长为2的正方形.
 为定值;
为定值; (a>b>0)的左、右焦点分别为
(a>b>0)的左、右焦点分别为 ,短轴两个端点为.A、B且四边形
,短轴两个端点为.A、B且四边形 是边长为2的正方形.
是边长为2的正方形.
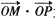 为定值;
为定值;