题目内容
如图,已知直角坐标系内有一条直线和一条曲线,这条直线和x轴、y轴正半轴分别交于点A和点B,且OA=OB=1.这条曲线是函数y=| 1 | 2x |
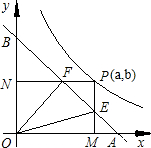 一点,它的坐标是(a、b),由点P向x轴、y轴所作的垂线PM、PN,垂足是M、N,直线AB分别交PM、PN于点E、F.
一点,它的坐标是(a、b),由点P向x轴、y轴所作的垂线PM、PN,垂足是M、N,直线AB分别交PM、PN于点E、F.(1)分别求出点E、F的坐标(用a的代数式表示点E的坐标,用b的代数式表示点F的坐标,只须写出结果,不要求写出计算过程);
(2)求△OEF的面积(结果用含a、b的代数式表示);
(3)分别计算AF与BE的值(结果用含a、b的代数式表示);
(4)△AOF与△BOE是否一定相似,请予以证明;如果不一定相似或一定不相似,简要说明理由.
分析:(1)根据图示知,点F的纵坐标是b,横坐标是OB-ON=1-a;点E的纵坐标是OA-AM=1-a,横坐标是a;
(2)利用割补法求得S△EOF=S矩形MONP-S△EMO-S△FNO-S△EPF;
(3)根据相似三角形的判定定理SAS证明△AOF∽△BOE.
(2)利用割补法求得S△EOF=S矩形MONP-S△EMO-S△FNO-S△EPF;
(3)根据相似三角形的判定定理SAS证明△AOF∽△BOE.
解答:解:(1)点E(a,1-a),点F(1-b,b);(2分)
(2)S△EOF=S矩形MONP-S△EMO-S△FNO-S△EPF,
=ab-
a(1-a)-
b(1-b)-
(a+b-1)2,
=
(a+b-1);(4分)
(3)BE=
=
a,
AF=
=
b;(6分)
(4)△AOF∽△BEO,(7分)
证明:∵OA=OB=1,
∴∠FAO=∠EBO;
∵点P(a,b)是曲线y=
上一点,
∴2ab=1,即AF•BE=1;
又∵OA•OB=1,
∴
=
;
∴△AOF∽△BEO.
(2)S△EOF=S矩形MONP-S△EMO-S△FNO-S△EPF,
=ab-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
(3)BE=
| a2+(1-1+a)2 |
| 2 |
AF=
| (1-1+b)2+b2 |
| 2 |
(4)△AOF∽△BEO,(7分)
证明:∵OA=OB=1,
∴∠FAO=∠EBO;
∵点P(a,b)是曲线y=
| 1 |
| 2x |
∴2ab=1,即AF•BE=1;
又∵OA•OB=1,
∴
| AF |
| OB |
| OA |
| BE |
∴△AOF∽△BEO.
点评:本题主要考查了反比例函数的综合题、相似三角形的判定及勾股定理.解答(4)题时,利用反比例函数图象上的点的特点,图象上所有的点都满足函数解析式.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
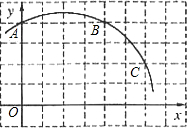 如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.
如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C. 12、如图,已知直角坐标系中的点A、B的坐标分别为A(2,4)、B(4,0),且P为AB的中点.若将线段AB向右平移3个单位后,与点P对应的点为Q,则点Q的坐标是( )
12、如图,已知直角坐标系中的点A、B的坐标分别为A(2,4)、B(4,0),且P为AB的中点.若将线段AB向右平移3个单位后,与点P对应的点为Q,则点Q的坐标是( ) 7、如图,已知直角坐标系中一条圆弧经过正方形网格的格点A,B,C.若A点的坐标为(0,4),D点的坐标为(7,0),那么圆心M点的坐标( )
7、如图,已知直角坐标系中一条圆弧经过正方形网格的格点A,B,C.若A点的坐标为(0,4),D点的坐标为(7,0),那么圆心M点的坐标( )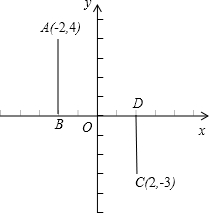 如图,已知直角坐标系中四点A(-2,4),B(-2,0),C(2,-3),D(2,0)、设P是x轴上的点,且PA、PB、AB所围成的三角形与PC、PD、CD所围成的三角形相似,请写出所有符合上述条件的点P的坐标:
如图,已知直角坐标系中四点A(-2,4),B(-2,0),C(2,-3),D(2,0)、设P是x轴上的点,且PA、PB、AB所围成的三角形与PC、PD、CD所围成的三角形相似,请写出所有符合上述条件的点P的坐标: 如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.用直尺和圆规画出该圆弧所在圆的圆心M的位置(不用写作法,保留作图痕迹).
如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.用直尺和圆规画出该圆弧所在圆的圆心M的位置(不用写作法,保留作图痕迹).