题目内容
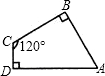 在四边形ABCD中,∠C=120°,∠B=∠D=90°,CD=3,BC=12,则四边形ABCD的面积为________.
在四边形ABCD中,∠C=120°,∠B=∠D=90°,CD=3,BC=12,则四边形ABCD的面积为________.


分析:延长BC交AD于点E,根据已知条件可求出△ABE和△CDE的面积,两者面积相减可求出四边形ABCD的面积.
解答:
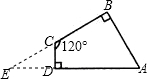 解:延长BC,与AD的延长线交于点E,
解:延长BC,与AD的延长线交于点E,∵∠BCD=120°,
∴∠DCE=60°,
在Rt△CDE中,CD=3,∠DCE=60°,
∴∠E=30°,EC=
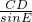 ,
,∴EC=6,
∵BC=12,
∴BE=12+6=18.
在Rt△ABE中,∠E=30°,BE=18,
则AB=6
 ,
,S△ABE=18×6
 ×
× =54
=54 ,
,S△CDE=ED×CD×
 =3×3
=3×3 ×
× =
=
 ,
,S四边形ABCD=S△ABE-S△CDE=54
 -
-
 =
=
 .
.故填空答案:

 .
.点评:本题考查对多边形面积的求法,通过作辅助线可将问题进行转化,两个直角三角形面积相减可即所求四边形的面积.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 11、如图所示,在四边形ABCD中,BD是它的一条对角线,若∠1=∠2,∠A=55°16′,则∠ADC=
11、如图所示,在四边形ABCD中,BD是它的一条对角线,若∠1=∠2,∠A=55°16′,则∠ADC=
 如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是边DC的中点,N是边AB的中点.△MPN是什么三角形?为什么?
如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是边DC的中点,N是边AB的中点.△MPN是什么三角形?为什么?