题目内容
如图,已知AB为⊙O的直径,CD是弦,且AB CD于点E.连接AC、OC、BC.
CD于点E.连接AC、OC、BC.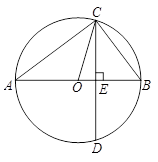
(1)求证:∠ACO=∠BCD.
(2)若BE=3,CD=8,求⊙O的直径.
证明:(1)∵AB为⊙O的直径,CD是弦,且AB CD于E,
CD于E,
∴CE=ED, 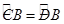
∴ BCD=
BCD= BAC.
BAC.
∵OA=OC,
∴ OAC=
OAC= OCA .
OCA .
∴ ACO=
ACO= BCD.
BCD.
(2) ∵CD=8,
∴CE=ED=4,
在Rt BCE中,
BCE中,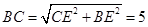 .
.
∵AB为⊙O的直径,
∴∠ACB=∠BEC=90°.
∵∠B=∠B,
∴△CBE∽△ABC.
∴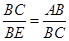 .
.
∴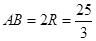
答:⊙O的直径为 .
.
解析试题分析:(1)根据垂径定理得出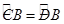 ,根据圆周角定理得出∠BCD=∠CAB,根据等腰三角形的性质得出∠CAB=∠ACO,即可得出答案;(2)根据垂径定理求出CE,根据勾股定理求出BC,证出△BCE和△BCA相似,即可得出比例式,代入计算即可求出答案.
,根据圆周角定理得出∠BCD=∠CAB,根据等腰三角形的性质得出∠CAB=∠ACO,即可得出答案;(2)根据垂径定理求出CE,根据勾股定理求出BC,证出△BCE和△BCA相似,即可得出比例式,代入计算即可求出答案.
考点:垂径定理;勾股定理;等腰三角形性质;相似三角形的性质和判定.
点评:本题主要考查了相似三角形的性质和判定,圆周角定理,垂径定理,等腰三角形性质,勾股定理等知识点的应用,解答本题的关键是培养学生综合运用定理进行推理和计算的能力.

练习册系列答案
相关题目
如图,过⊙O内一点M的最长弦长为12cm,最短弦长为8cm,那么OM长为( )
| A.6cm | B. cm cm | C. cm cm | D.9cm |
三角形的外心是( )
| A.各内角的平分线的交点 | B.各边中线的交点 |
| C.各边垂线的交点 | D.各边垂直平分线的交点 |
 ,并任选一个你喜欢的数x代入求值.
,并任选一个你喜欢的数x代入求值.

 与
与 相切于点
相切于点 ,线段
,线段 交
交 .过点
.过点 交
交 ,连接
,连接 ,且
,且 交
交 于点
于点 .若
.若 .
.
 与弧
与弧 所围成的阴影部分的面积.(结果保留
所围成的阴影部分的面积.(结果保留 )
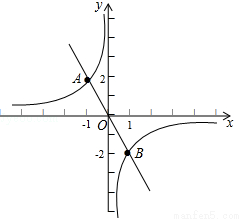
)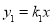 和反比例函数
和反比例函数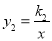 的图象交于A(﹣1,2)、B(1,﹣2)两点,若
的图象交于A(﹣1,2)、B(1,﹣2)两点,若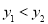 ,则x的取值范围是 .
,则x的取值范围是 .